세상에서 가장 아름다운 수학 등식, 오일러 공식을 증명해 보자
세계의 수많은 수학자, 과학자들이 여러 가지 수학 등식 중에서 유연성, 단순성, 미적 매력 등의 이유로 세상에서 가장 아름다운 수학 공식이라고 알려진 수식이 있습니다.
제가 이전 글에서 몇 번 언급한 적이 있는 바로 오일러 공식 또는 오일러 등식이라고 알려진 다음 식입니다.

위 등식을 자세히 보면, 일명 문과생은 e를 고등학교까지는 배우지 않은 수입니다. 이것에 관한 내용은 다음 글에서 참고할 수 있습니다.
https://nous-temperature.tistory.com/667
자연상수 e, 무리수 e 계산 해 보기
고등학교 다닐 때 선택한 문과로 인해, 가장 이해할 수 없었던 것이 e라는 숫자였습니다. 이 숫자의 의미를 그 당시 대강은 알고 있었지만, 문과에서는 나오는 경우가 없었으므로 기억 속에 사라
nous-temperature.tistory.com
자연상수 e에 관한 개념을 위의 글을 통해서 이해했다면, 이제 오일러 공식은 조금 이해할 수 있습니다. 인위적으로 만들어진 수인 e, 자연수가 아닌 허수 i, 원주율, 자연수의 시작의 숫자인 1로 이루어진 식을 더하면, 0이 된다는 이 식은, 전혀 연관성이 없어 보이는 5개라는 숫자로 이루어진 이 공식이 왜 아름다운지는 저는 아직까지 이해하기 어려운 과제 중의 하나입니다.
이 공식을 증명하는 여러 가지 방법이 있는 줄 알지만, 지금까지 제가 수학 이야기에서 쓴 몇 개의 글을 통해서 이 등식을 어설프게 증명할 수 있을 듯하여 글을 써 보고자 합니다.
먼저, 제가 블로그를 시작하면서 초창기에 썼던 삼각함수에 관한 글이 있습니다.
https://nous-temperature.tistory.com/16
[삼각함수] sin, cos, tan 표 값 구하기 (20년이 지나도 잊지 않는 방법)
이번 시간에는 삼각함수 sin, cos, tan값을 잊어버리지 않고 오래 기억하는 방법을 알아보겠습니다. 고등학교를 졸업한지 꽤 많은 세월이 흘렀고, 수학을 전공하지 않은 제가 최근까지 누구에게
nous-temperature.tistory.com
위 글에서 저는 단위원(반지름이 1인 원)을 이용하여 sin, cos, tan 값을 구하는 방법을 설명했습니다. 이 글의 내용을 자세히 보면, 어떠면 가장 핵심적인 부분은 반지름이 1일 때, x, y 축 좌표 평면에서 x 값의 좌표는 cos 값이 되고, y값의 좌표는 sin 값이 된다는 것일지 모릅니다. x, y 축이 모두 실수 범위이긴 하지만, 이 평면 좌표를 허수인 i를 y축으로 두고, 각을 θ라는 복소평면을 만들면, 다음과 같은 그래프를 그릴 수 있습니다.

이때 원과 각 세타로 이어진 직선과 만나는 점을 P라고 한다면, 이 P는 복소수로 나타낼 수 있으며, 실수 축 좌표를 a, 허수 축 좌표를 b라고 한다면, P는 다음과 같이 나타낼 수 있습니다. 즉, a+bi로 말이죠.

단위 원에서 x축은 cosθ, y축은 sinθ이므로 위 그래프는 다음과 같이 쓸 수 있겠습니다.

cosθ + isinθ를 θ에 관한 함수로 표현하면 다음과 같이 쓸 수 있습니다.
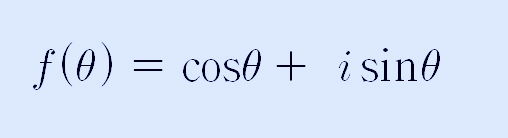
이 함수에서 f(a) = cosa+isina로 쓸 수 있고, f(b) = cosb+isinb로 쓸 수 있고, f(a)와 f(b)의 곱은 다음과 같이 쓸 수 있습니다.
f(a) x f(b) = (cosa+isina)(cosb+isinb)
위 식을 전개해 보도록 하겠습니다.
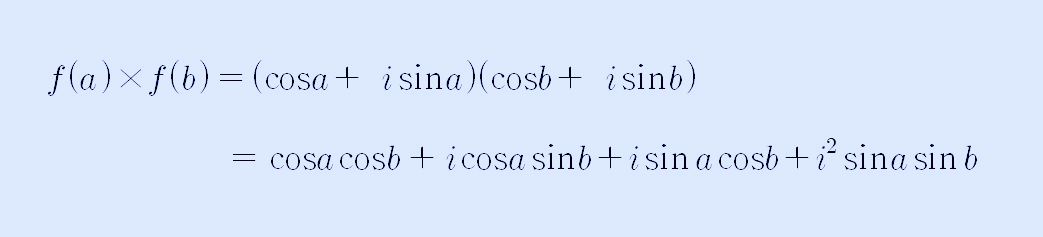
위 결과에서 i의 제곱은 -1이므로 다음과 같이 정리할 수 있습니다.
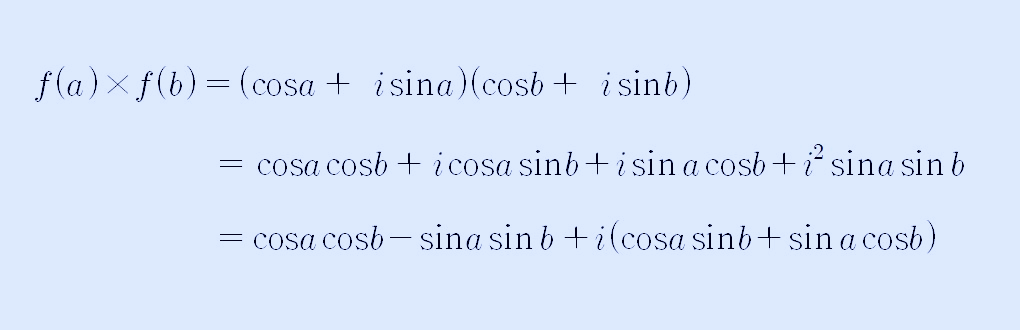
여기까지 계산하니 흥미로운 것이 보입니다. sin, cos 덧셈 정리에 의해서 위에서 정리한 식은 다음과 같이 쓸 수 있습니다. cos, sin 덧셈 정리는 다음 글에서 확인할 수 있습니다.
https://nous-temperature.tistory.com/573
삼각함수 덧셈정리 증명
삼각함수의 합차 공식을 증명하는 방법의 한 가지를 알아보겠습니다. 삼각함수 덧셈 정리, 뺄셈 정리는 증명이 끝나는 마지막에 정리하였으니, 결과를 바로 알고 싶으시다면 맨 아래를 보시면
nous-temperature.tistory.com
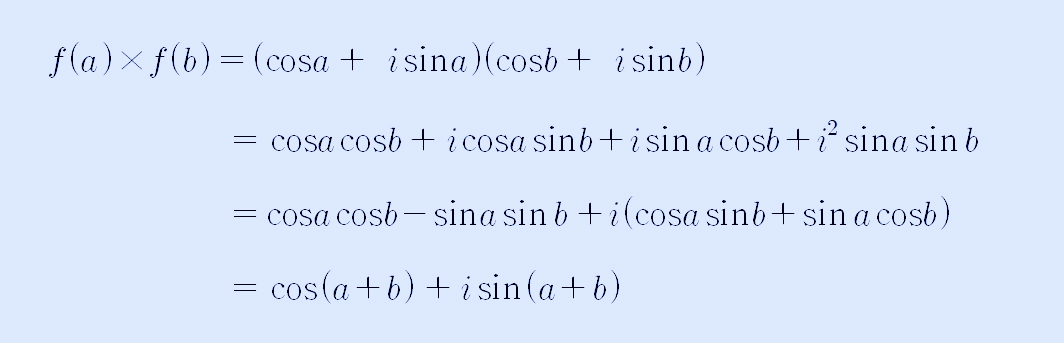
위에서 f(θ) = cosθ + isinθ라고 했는데, θ 대신에 a+b를 대입하면 다음과 같습니다.
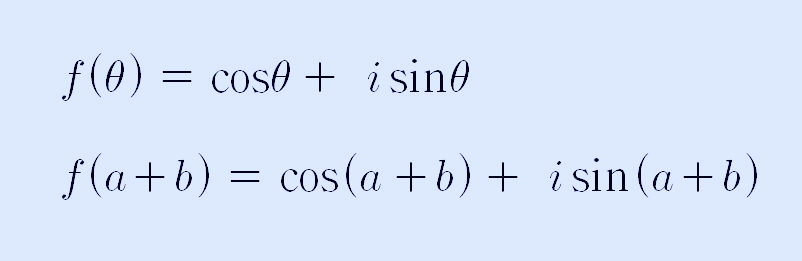
여기까지 정리하고 보니, f(a) x f(b)의 값이 f(a+b)의 값과 같게 되었으며 다음과 같이 쓸 수 있습니다,.
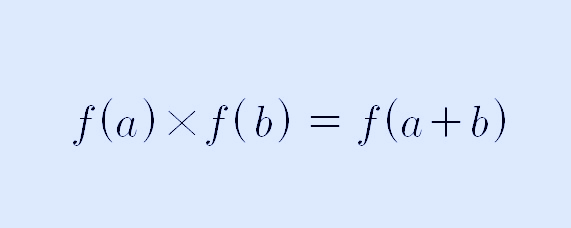
위 식에서 a와 b가 같다면, 위 식은 다음과 같이 쓸 수 있습니다.
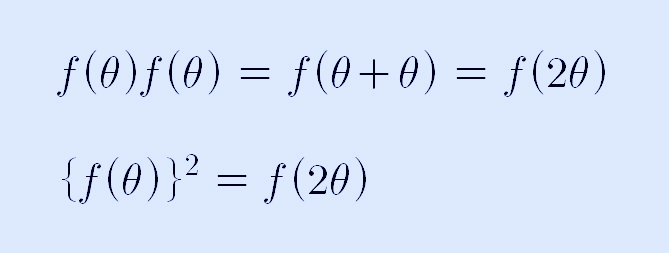
이번에는 f(θ)의 역수에 관해서 알아보도록 하겠습니다. 위에서 정리한 식을 적용하면 다음과 같이 쓸 수 있습니다.
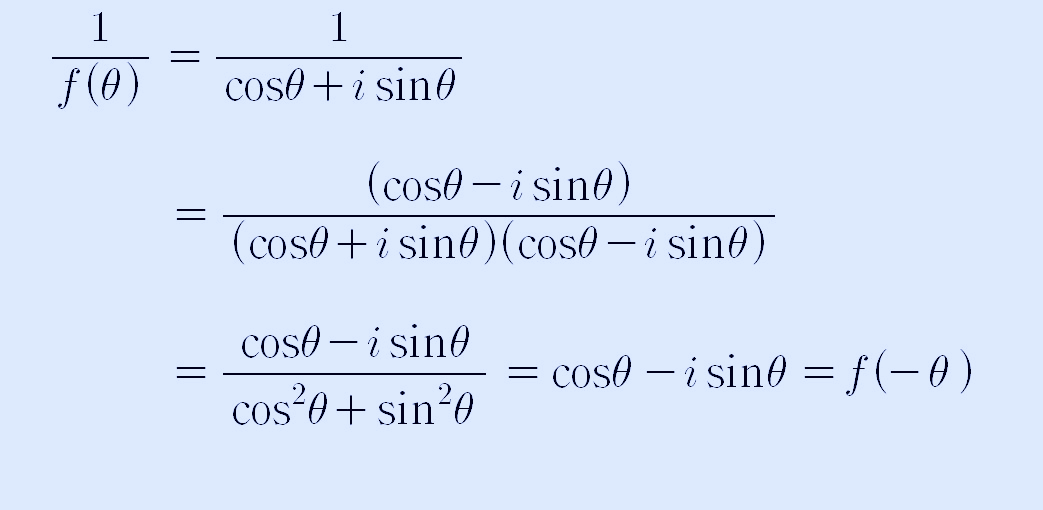
cosθ - isinθ는 삼각함수의 각 변환 공식을 적용하면, f(-θ)가 되는데, cos(θ) = cos(-θ), sin(-θ) = -sin(θ) = 이기 때문입니다.
θ = 0일 때, f(0)의 값은 다음과 같이 계산할 수 있습니다.
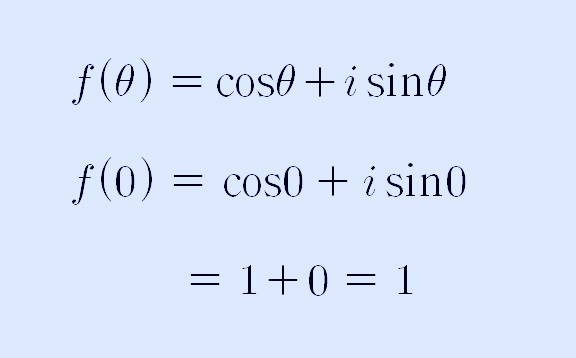
이제, f(θ) = cosθ + isinθ 식을 θ에 대해서 미분해 보도록 하겠습니다. 그러면 다음과 같은 식으로 정리할 수 있습니다.
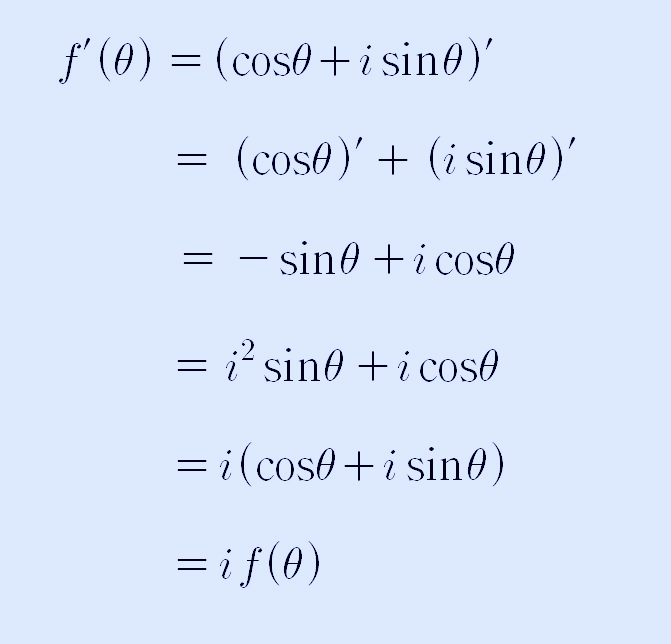
지금까지 구한 식을 정리하면 다음과 같이 5가지로 나타낼 수 있습니다.
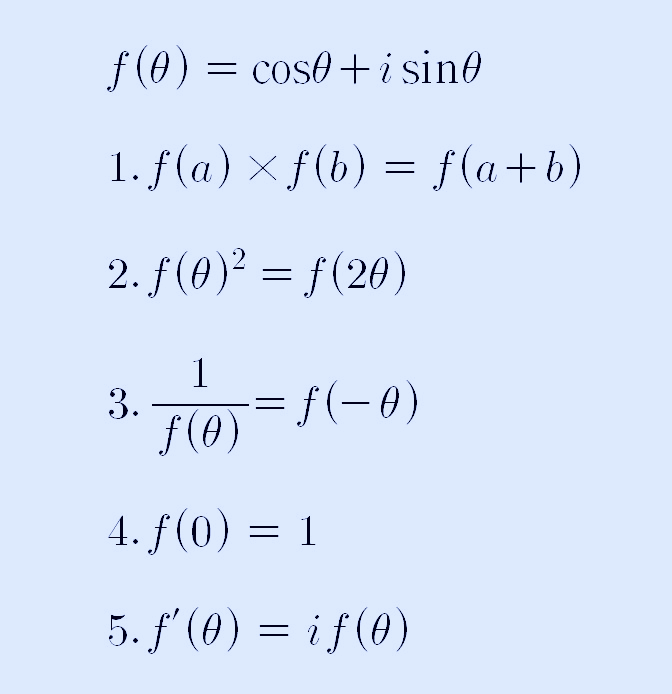
위의 5가지 성질을 자세히 보면, 오일러 상수 e를 밑으로 하는 e의 x제곱인 수와 비교해 보도록 하겠습니다.
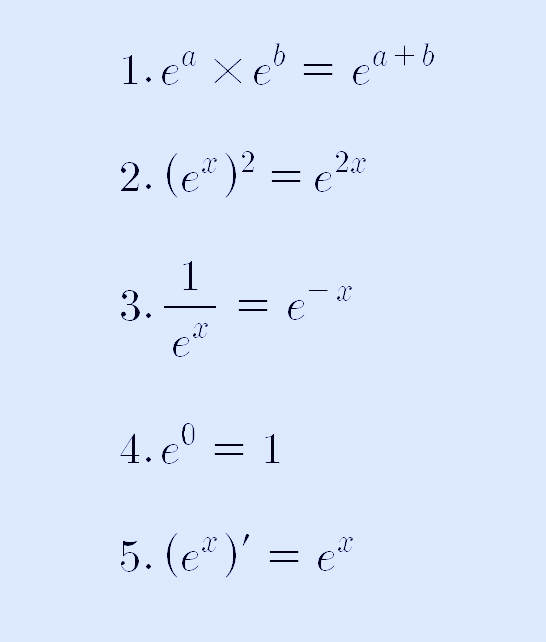
놀랍게도 위의 1~4번째 식까지 f(θ) 함수와 e의 x제곱인 수의 특징이 정확하게 일치하네요. e의 x제곱인 수의 특징에서 e의 ix의 특징으로 놓고 보면, 이제; 1~5번째 특징이 다음과 정확하게 일치합니다.
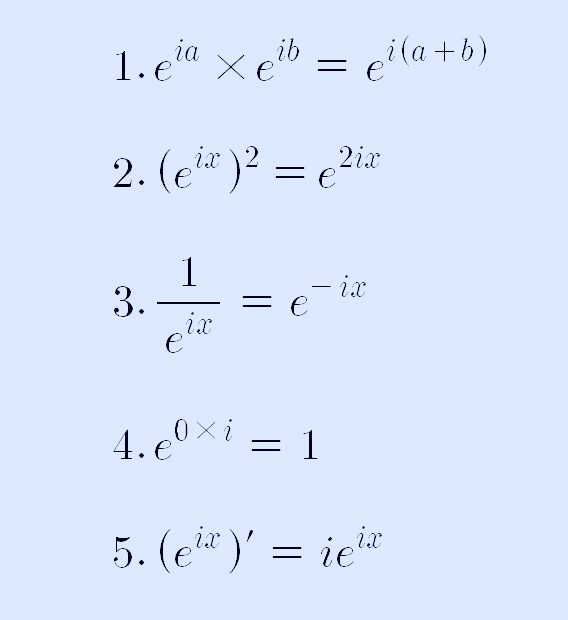
즉, 복소평면에 만들어진 함수는 e의 ix 제곱의 함수는 같은 함수이다는 것을 알 수 있으며, 따라서 다음과 같은 식을 쓸 수 있습니다. 바로 오일러 공식입니다.
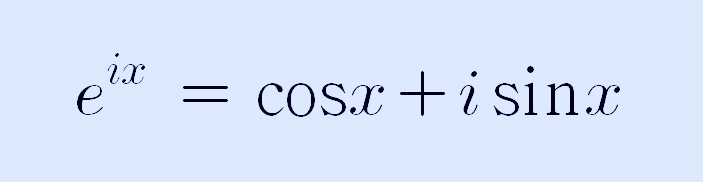
만약에 x를 파이라고 한다면 위의 식은 다음과 같이 정리할 수 있습니다.
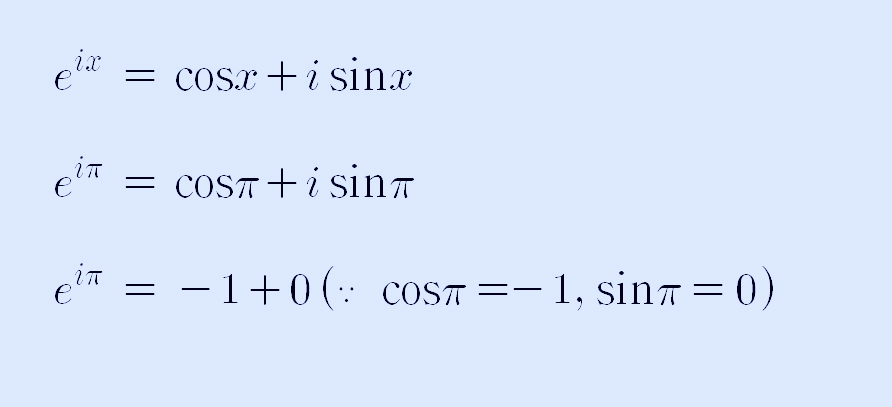
이제 마지막 -1을 좌변으로 이동시키면, 오일러 등식이 최종적으로 다음과 같이 정리할 수 있습니다.
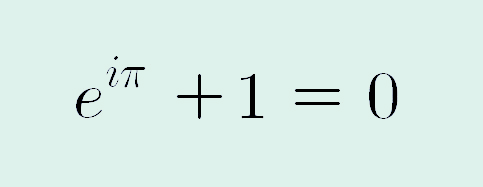
충분히 검토했다고 생각하지만, 혹시 중간에 계산이 틀렸거나, 부호 등이 다르 경우가 있다고 알려주시면 검토 후 수정하도록 하겠습니다. 이상으로 오늘 글을 마칩니다.
