삼각함수 덧셈정리 증명
삼각함수의 합차 공식을 증명하는 방법의 한 가지를 알아보겠습니다.
삼각함수 덧셈 정리, 뺄셈 정리는 증명이 끝나는 마지막에 정리하였으니, 결과를 바로 알고 싶으시다면 맨 아래를 보시면 되겠습니다.
삼각함수 덧셈 정리를 증명하는 법은 x, y축에 단위원(반지름 1)으로 그려서 할 수 있습니다.

삼각형 PQO에서 점 P의 좌표는 호도법에 의해서 (cos𝛂, sin𝛂), Q의 좌표는 (cos𝛃, sin𝛃)로 쓸 수 있습니다.
두 점의 좌표를 알 때, 두 점 사이의 거리의 제곱은 두 점의 x좌표의 차의 제곱과 y좌표의 차의 제곱의 합과 같기 때문에 다음과 같은 식으로 정리할 수 있습니다.
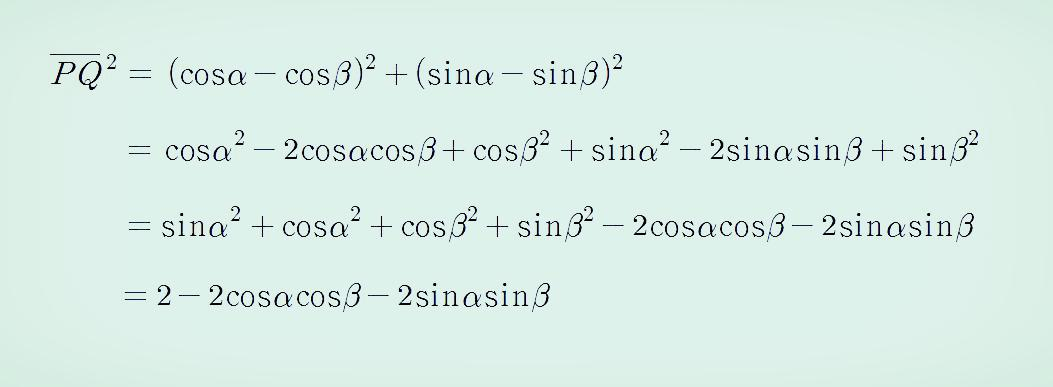
선분 OP와 선분 OQ는 원의 반지름의 길이인 1이므로 삼각형 PQO에서 코사인 제2법칙을 적용하면 다음과 같이 쓸 수 있습니다.

위의 첫 번째 결과와 두 번째 결과는 같아야 하므로 다음과 같이 쓸 수 있습니다. 이렇게 하면 코사인 뺄셈 공식을 아래와 같이 증명할 수 있습니다.
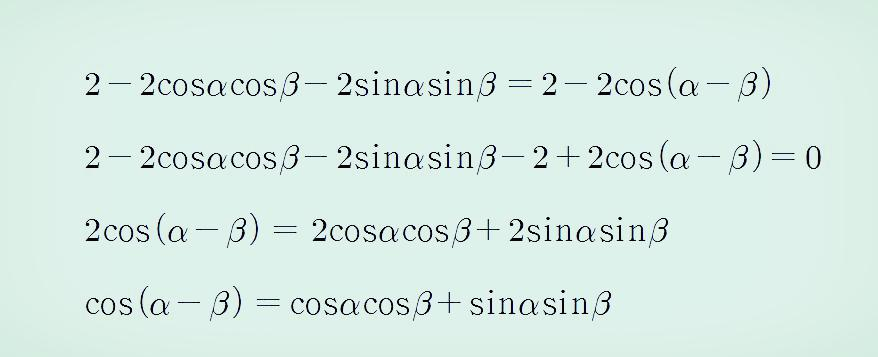
코사인 뺄셈 공식이 다음과 같이 계산되었습니다.
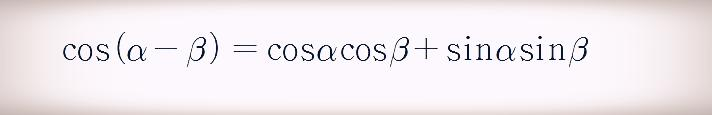
위 식을 이용하면 나머지 삼각함수 합차 공식을 모두 증명할 수 있습니다.
먼저, 코사인 덧셈 공식을 증명하기에 앞서 삼각함수 성질에 관해서 알아보겠습니다. 아래와 같이 삼각함수의 음수 값은 다음과 같습니다.

코사인 뺄셈 공식에서 𝛃를 음수로 바꾼 후, 위 성질을 적용하면 코사인 덧셈 공식은 다음과 같이 다음과 같이 정리할 수 있습니다.

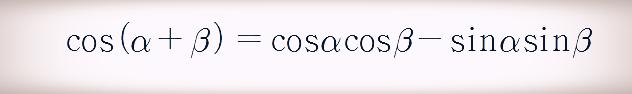
이제 사인 뺄셈 공식을 유도해 보겠습니다. 사인 뺄셈 공식을 유도하기 앞서 삼각함수는 또 다음과 같은 성질이 있다는 것을 알고 있어야 합니다.
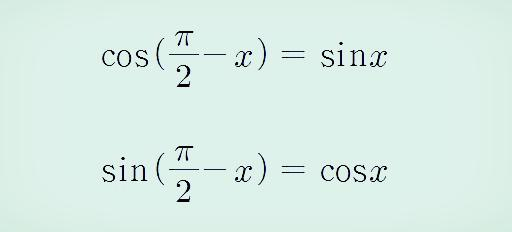
코사인 덧셈 공식에서 알파는 "2분의 파이 -알파"로 놓고 식을 정리하면 사인 뺄셈 공식은 다음과 같이 유도됩니다.
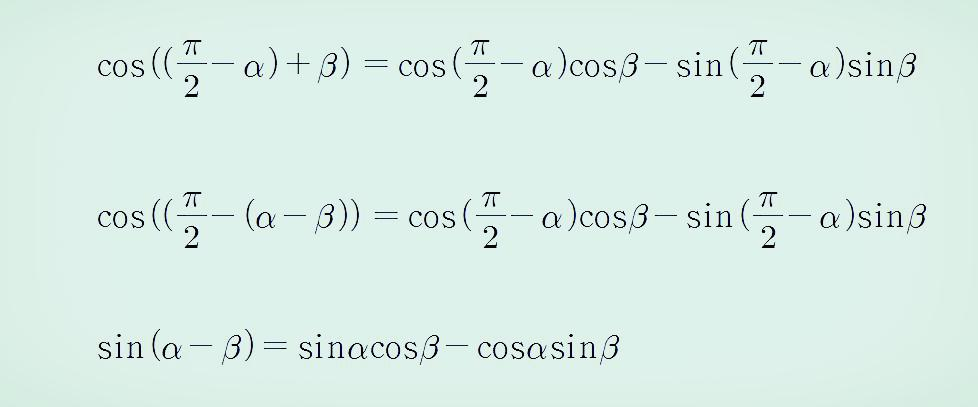

사인 덧셈 공식은 위의 사인 뺄셈 공식을 이용해서 다음과 같이 구할 수 있습니다.


이제 탄젠트 합 공식을 구해보도록 하겠습니다. 맨 위 단위원 그림에서 호도법과 삼각비에서 탄젠트 값은 아래와 같이 코사인과 사인 값으로 쓸 수 있습니다.

만약에 x를 "알파+베타"라고 한다면, 탄젠트 합 공식은 위의 식과 사인과 코사인 덧셈 공식을 사용해서 다음과 같이 구할 수 있습니다.

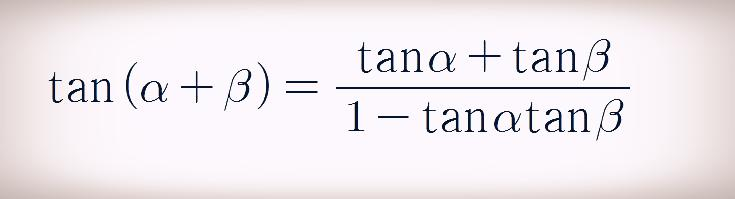
마지막으로 탄젠트 뺄셈 공식은 다음과 같이 유도할 수 있습니다.

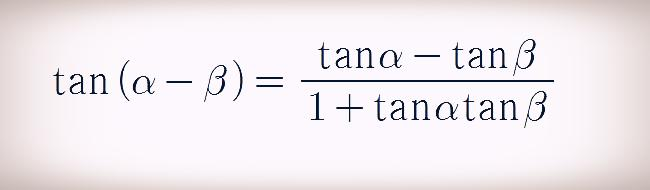
위에서 구한 삼각함수의 합차 공식을 정리하면 다음과 같습니다.


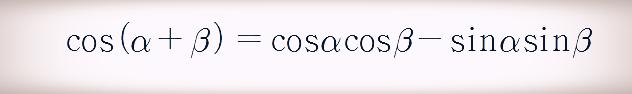
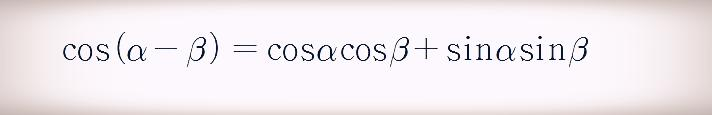
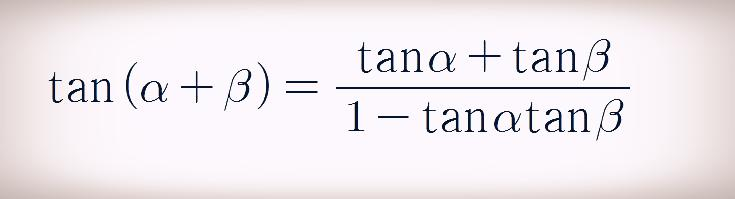
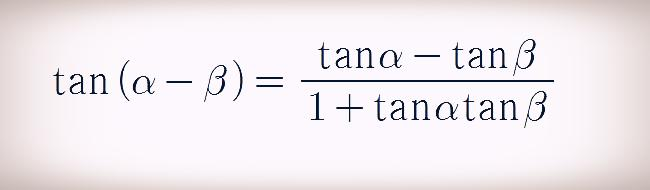
이상으로 삼각함수 합차 공식 유도 설명을 마칩니다.
'수학 이야기' 카테고리의 다른 글
| 1+1=0 증명? (2) | 2021.08.06 |
|---|---|
| 헤론의 공식 증명 (0) | 2021.07.16 |
| 수열 실생활 활용 사례 - 피보나치 수열 (2) | 2021.07.05 |
| 서울에 미용실 수는 몇 개? (3) | 2021.06.20 |
| 삼차함수 접선 넓이 공식 구하기 (4) | 2021.03.30 |






