한평 크기, 면적은 길이가 몇 미터? 루트 2 값 계산으로 알아보기
우리나라에서 넓이 단위는 법정 계량 단위인 제곱미터(m²)를 쓰는 것을 원칙으로 삼고 있습니다. 하지만, 일상생활에서 유독 "평"이라는 단위를 사용하는 경우가 많습니다. 공식적으로 법정 계량 단위를 의무적으로 쓰는 것이 얼마 되지 않았기에 언론이나 분양 공고 등을 보면 제곱미터를 쓰기는 하지만, 여러 가지 방법으로 "평"이라는 용어도 (어디엔 가에 숨겨 놓고 같이 쓰는) 경우가 많습니다.
하지만, 제곱미터에 익숙한 아이들이 "평"이라는 말을 일상생활에서 접하곤 길이가 얼마나 되는 것인지 묻고 합니다.
많은 분들이 알고 있는 것처럼 한 평은 3.3m²입니다. 이렇게만 말하면 아이들은 두 변의 길이 얼마인 사각형의 넓이인지 다시 묻습니다.
이번 시간에는 3.3 제곱미터인 넓이의 정사각형이 있다고 할 때, 한 변의 길이가 얼마인 지를 알아보고자 합니다.
이를 계산하는 방법에 들어가기 앞서 루트 2의 값을 계산해 보도록 하겠습니다. 만약에 루트 2가 정사각형의 넓이라면 이 한 변을 구하는 방법과 같은 말이 됩니다.

넓이가 루트 2인 정사각형은 가로와 세로의 길이가 같기 때문에 한 변의 길이를 x라고 한다면 넓이를 구하는 식은 다음과 같이 쓸 수 있습니다,.
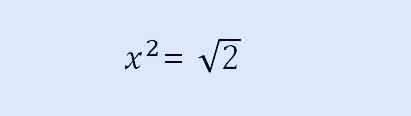
위 식에서 어떤 수 x를 제곱하면 루트 2가 되는 값을 구하면 되는데, 보통 다음과 같이 나눗셈을 응용해서 구할 수 있습니다.
먼저, 다음과 같이 루트 기호를 길게 그려 줍니다.

그러고 나서 어떤 양수를 제곱해서 2 이하인 수를 찾습니다. 1을 제곱하면 1, 2를 제곱하면 4이므로 2 이하인 1을 나눗셈처럼 써 줍니다.

그런 다음, 1을 제곱한 수를 2 밑에 써 줍니다. 나눗셈처럼 써 줍니다. 나눗셈을 응용한 것이므로 2에서 1을 뺀 수를 나눗셈처럼 써 줍니다.

이제, 1을 루트 2 앞에 다음과 같이 차례로 두 번씩 써 주고 더한 값인 2를 씁니다.

이제 몫인 1과 루트 2 다음에 소수점을 쓰고, 소수점 이하에서 10의 제곱이 될 수 있도록 0을 두 개 써 줍니다. 그러면 다음과 같이 나눗셈처럼 빼서 나온 아래에도 0을 두 개 쓰면 다음과 같은 모습이 됩니다.

이제, 왼쪽에 있는 2 다음에 십의 자리를 만들어 주기 위해 네모를 하나 넣고, 아래에도 하나 넣습니다. 또한 몫으로 간주되는 루트 위에 있는 1. 다음에도 동일한 네모를 한 개 넣습니다. 그러면 다음과 같은 식의 모습이 됩니다.

위 식에서 왼쪽에 있는 네모와 루트 위에 있는 네모에 같은 수를 넣고, 이를 곱했을 때, 100이 넘지 않은 최대의 수를 찾습니다. 만약에 네모에 3을 넣으면 23x3 = 69이고, 4를 넣으면 24x4 = 96이고, 5를 넣으면 25x5=125이므로 100을 넘지 않은 최대의 수가 되려면 4이므로 네모에는 모두 4를 넣습니다. 그리고 곱한 값을 아래 100 밑에 써 줍니다. 다음과 같이 말이죠.

이제 다시 처음에 했던 절차대로 똑같이 반복하면 됩니다. 100에서 96을 뺀 수를 써 주고, 루트 안에는 0을 두 개 더 써 주고, 왼쪽에는 24와 4를 더한 수를 써 주고 네모를 붙여 주면 다음과 같은 식이 됩니다.

이제 왼쪽 28 다음에 있는 네모와 루트 위 4 다음에 있는 네모에 동일한 수를 넣고 곱했을 때, 아래 400을 넘지 않은 최대의 숫자를 써 줍니다. 281 x 1 = 281이 되고, 282 x 2 = 564가 되기 때문에 400을 넘지 않은 수는 1이므로 네모에 모두 1을 써 줍니다.

이후에도 계속 같은 방식으로 계산하면 됩니다. 네모를 붙여 주고, 0을 두 개 쓰고 계속 계산해서 나가면 됩니다.

위의 네모에는 4가 들어가야 11900을 넘지 않으면서 최대의 수가 됩니다.
이와 같은 방식으로 루트 2의 값은 1.414......로 나오는 값을 끝없이 구할 수 있습니다. 참고로 루트 2는 무리수입니다.
루트 2의 값을 계산하는 방식으로 한 평의 넓이인 3.3 제곱미터(m²)의 한 변의 길이도 구할 수 있습니다. 루트 안에 2 대신에 3.3이 들어가는 것만 차이가 납니다. 계산하면 다음과 같이 쓸 수 있겠네요.

위식에서 마지막 네모에는 6이 들어가면 되겠습니다. 루트 3.3도 무리수이므로 계산은 끝없이 할 수 있겠습니다.
이제 한평 3.3 제곱미터는 한 변의 길이가 약 1.8m가 되겠습니다. 180cm인 사람의 키 길이로 정사각형을 만든다고 가정하면 한 평이 된다고 보시면 되겠습니다.
우리나라에서 현대 자동차 중에서 그랜저가 있습니다. 이 차의 전장은 4,900mm이고 전폭이 1,875mm인데 이를 미터로 바꾸면 전장 4.9m, 전폭 1.875m입니다. 이 직사각형의 넓이는 9.1875m²가 됩니다. 만약 이 넓이를 평으로 나타낸다면 9.1875를 3.3으로 나누면 평이 나오므로 약 2.784평이 됩니다. 3평이 약간 안 되는 면적이네요.
이 자동차 대수로 적용해 보면 자동차 10대가 약 27.8평이 되므로 아파트나 주택의 넓이를 어림잡아 비교해 볼 수가 있겠습니다. 자동차 11대면 30평이 약간 안 되며, 32평은 11대가 넘는 면적과 열추 비슷합니다.
이상으로 루트 2 값을 계산하는 법을 통해서 한 평의 한 변의 길이가 어느 정도 되는지를 살펴보았습니다.
'수학 이야기' 카테고리의 다른 글
| 루트3 근사값 계산법과 무리수 증명 하기 (0) | 2022.03.20 |
|---|---|
| 루트 2 무리수 증명 (0) | 2022.03.17 |
| 삼차함수 계수 부호 결정하기 (0) | 2022.03.14 |
| 삼차함수 1대 루트3 증명 (0) | 2022.03.05 |
| sin15 도, cos15 도, tan15 도 값 알아보기 (0) | 2022.02.26 |






