삼차함수 1대 루트3 증명
극댓값과 극솟값을 가지는 삼차 함수는 몇 가지의 비율 관계를 유지합니다.
이번 글에서는 변곡점에서 극값의 길이와 변곡점에서 x축과 평행한 직선을 그었을 때, 삼차 함수와 만나는 곳까지의 길이 비가 1대 루트 3이 되는 것을 증명해 보도록 하겠습니다.

극댓값과 극솟값을 가지는 일반적인 삼차 함수가 있다고 가정해 보겠습니다.

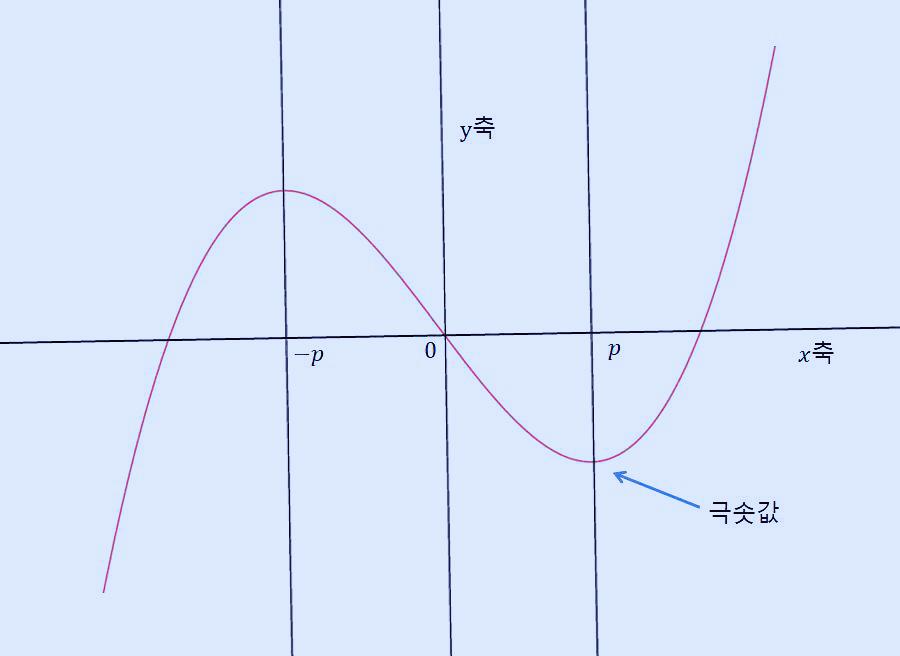
이 삼차 함수의 변곡점을 원점을 지난다고 가정하면 그래프 모양은 다음과 같습니다.

위 그래프에서 극솟값의 x 좌표를 p라고 하면 극댓값의 x 좌표는 -p가 됩니다. 삼차 함수는 변곡점에서 점대칭이기 때문에 아래와 같은 모습이 됩니다.
삼차 함수를 한 번 미분한 이차 함수의 근에서 극솟값과 극댓값을 가지므로 이른 그래프로 나타내면 다음과 같이 표현할 수 있습니다.

위 그래프를 삼차식과 이를 한번 미분한 값은 한 근이 p, 다른 한 근이 -p이고 2차 계수가 a이므로 이를 p로 정리하면 다음과 같이 쓸 수 있습니다.

위에서 계산한 f'(x) 값을 그래프에 정리하면 다음과 같습니다.

이제 위에서 구한 f'(x)를 f(x)로 전환하면 다음과 같이 정리할 수 있습니다.
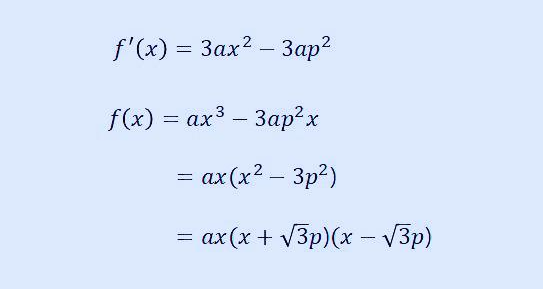
지금까지 구한 값을 위의 그래프에 넣으면 다음과 같이 쓸 수 있겠습니다.

위의 그래프에서 무엇인가가 보이나요?
그렇습니다. 삼차 함수의 근이 각각 0, 루트 3p, 마이너스 루트 3p이므로 이를 그래프에 나타내면 다음과 같이 쓸 수 있습니다.
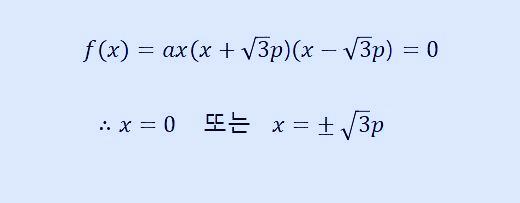

이제 다 구했습니다. 위 그래프를 보면 변곡점(원점)에서 극솟값과 극댓값까지의 거리는 각각 p가 되고, x축과 만나는 두 점까지의 거리는 각각 루트 3p이므로 이를 비율로 나타내면 다음과 같이 계산할 수 있습니다.

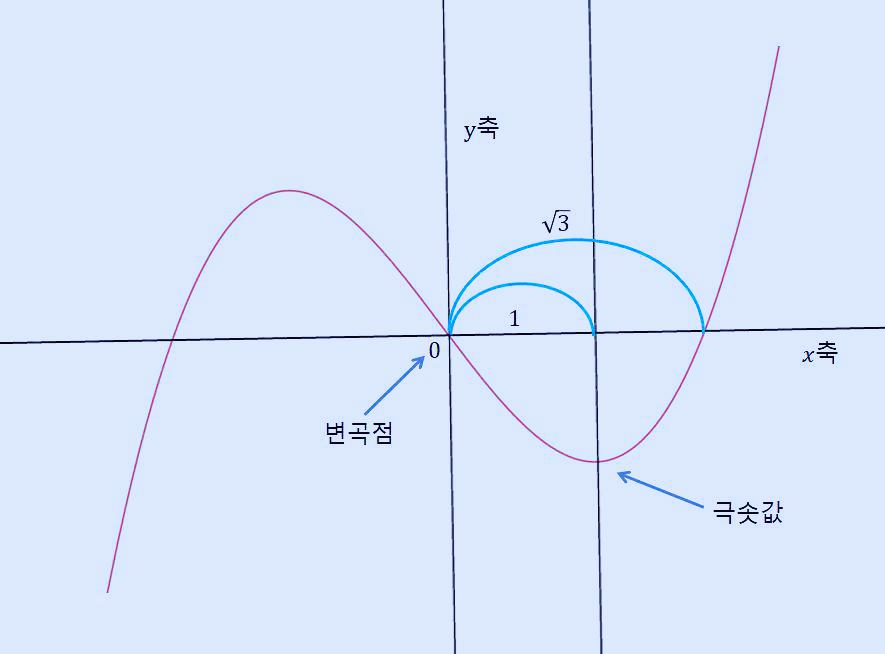
지금까지 삼차 함수에서 1대 루트 3이 되는 것이 무엇인지 살펴보았습니다.
'수학 이야기' 카테고리의 다른 글
| 한평 크기, 면적은 길이가 몇 미터? 루트 2 값 계산으로 알아보기 (1) | 2022.03.16 |
|---|---|
| 삼차함수 계수 부호 결정하기 (0) | 2022.03.14 |
| sin15 도, cos15 도, tan15 도 값 알아보기 (0) | 2022.02.26 |
| 2022 수능 생명과학2 오류 논란을 보면서 (2) | 2021.12.12 |
| 삼차함수 비율 관계를 증명해 보자 (0) | 2021.12.04 |






