2022 수능 생명과학2 오류 논란을 보면서
다음 수학 문제를 풀어 봅시다.
*한 변의 길이가 각각 루트 2, 루트 3, 루트 10인 아래와 같은 삼각형이 있을 때, cosA의 값을 구하시오.

이 문제는 이른바 코사인 제2법칙으로 계산할 수 있습니다.
삼각형이 위와 같은 모습일 때, 코사인 제2법칙은 다음과 같이 나타냅니다.

위 공식에 문제의 숫자를 대입해서 풀면, cosA 값을 구할 수 있습니다.

위 삼각형에서 a는 루트 3, b는 루트 10, c는 루트 2이므로 코사인 법칙에 숫자를 그대로 대입하면 다음과 같습니다.

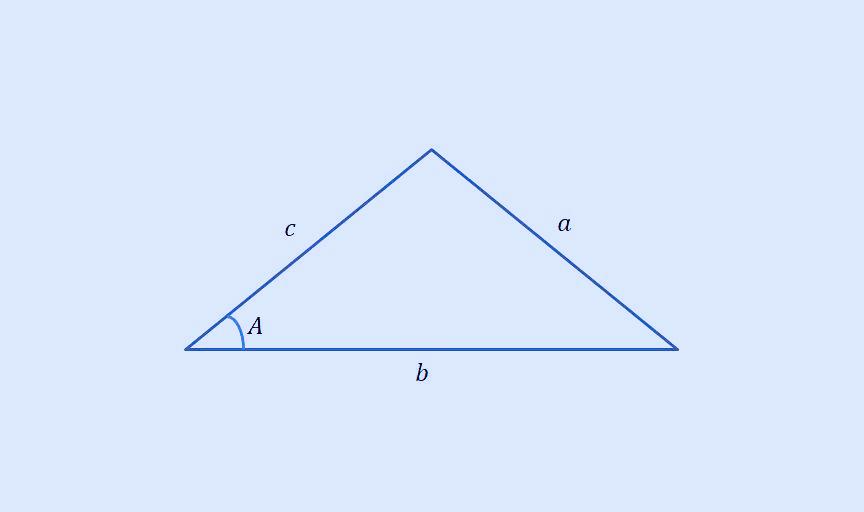
위 식을 한 번 더 계산하면 다음과 같습니다.
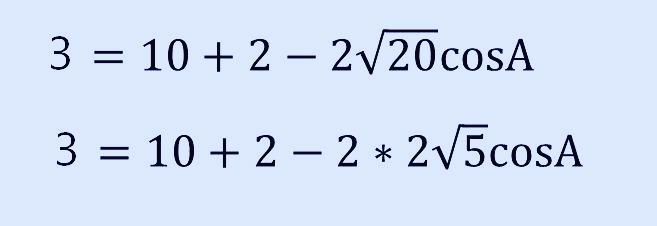
이제 뒤에 있는 2곱하기 2 루트 5 cosA를 계산하면 다음과 같이 쓸 수 있겠네요.
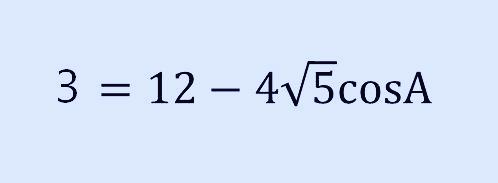
이제 cosA 값을 거의 다 구한 듯합니다. 아래와 같이 정리하면 구하고자 하는 cosA 값을 구할 수 있겠습니다.

지금까지 꽤 그럴듯한 삼각형의 cos 값을 구해 보았습니다. 누군가는 이 문제를 풀면서 말도 되지 않은 문제라는 것을 눈치챘을지도 모릅니다.
왜냐하면 길이가 루트 2, 루트 3, 루트 10인 세 변으로는 삼각형을 만들 수 없기 때문입니다. 루트 2와 루트 3을 더하면 루트 10보다 작기 때문에 삼각형이 될 수 없는 것이지요. 즉, 두 변을 더한 값을 나머지 한 변으로 뺀 값이 음수가 나오면 삼각형 자체가 되지 않기 때문에 이 문제는 성립할 수 없습니다.
하지만, 삼각형을 만들지 못하더라도 cos 법칙을 이용하여 그 값을 구할 수 있으므로 "학업 성취 수준을 변별하기 위한 평가 문항으로서의 타당성은 유지된다"고 한다면 그 누가 이 문제를 인정할 수 있겠습니까?
2022년 수능 생명과학 II 20번은 개체수가 음수가 나온다는 전제하에 문제가 구성되었다고 하는 뉴스를 보면서, 전공자는 아니지만 아무리 생각해 보아도 상식적으로 납득이 가지 않아 수학에서 생각나는 예시 하나를 제시해 보았습니다.
해당 문제가 오류라는 논란을 논외로 하더라도, "과학"이라는 어휘로 이루어진 교과목에서 모순되는 문제의 정답을 찾아야만 하는 교육적 현실이 그래서 서글프다는 생각을 하게 됩니다.
그냥 그렇다는 것입니다. 여러분의 생각은 어떠한가요?
'수학 이야기' 카테고리의 다른 글
| 삼차함수 1대 루트3 증명 (0) | 2022.03.05 |
|---|---|
| sin15 도, cos15 도, tan15 도 값 알아보기 (0) | 2022.02.26 |
| 삼차함수 비율 관계를 증명해 보자 (0) | 2021.12.04 |
| 삼차함수 변곡점 대칭 증명 (0) | 2021.12.03 |
| 2022 수능 수학 1번, 난감했다고 한다 (0) | 2021.11.28 |






