삼차함수 변곡점 대칭 증명
수학에서 변곡점이란 무엇을 말하는 것일까요?
변곡점을 한자로 쓰면 다음과 같습니다.
變曲點
變 변할 변
曲 굽을 곡
點 점 점
이를 글자 그대로 해석하면, ‘굽은 곳이 변하는 점’ 정도가 되겠습니다. 표준국어대사전에는 이를 확장해서 ‘굴곡의 방향이 바뀌는 자리를 나타내는 곡선 위의 점’이라고 정의되어 있네요.
영어로 변곡점은 inflection point라고 하는데, inflection은 ‘구부리다’는 대표적 의미가 있는 inflect의 명사형으로 ‘어떤 함수가 오목함이 변하는 점’이라는 뜻이 있습니다.
미적분학에서 변곡점은 ‘두 번 미분 가능한 함수에 대하여 함수의 그래프가 위로 볼록인 상태에서 아래로 볼록인 상태로 변하거나 아래로 볼록인 상태에서 위로 볼록인 상태로 변하는 점’을 말합니다. 다른 말로 하면, 두 번 미분한 함수의 부호가 바뀌는 점, 또는 두 번 미분한 값이 0이 되는 점이라고도 할 수 있습니다. 이를 수학식으로 나타내면 다음과 같습니다.

이러한 변곡점의 수학적 정의를 이용해서 삼차함수 변곡점이 대칭이 이유를 증명해 보도록 하겠습니다. 이를 하기 위해서는 함수의 대칭에 관해서 살펴보도록 하겠습니다.
∎ 함수의 평행이동
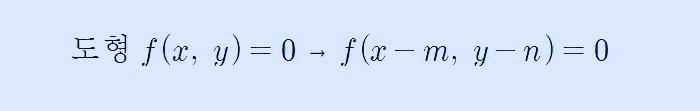
도형 f(x, y) = 0을 x축의 방향으로 m만큼, y축의 방향으로 n만큼 평행이동한 도형의 방정식은 f(x-m, y-n) = 0이 됩니다.
이 정의를 해석하는 방법은 f 안에 있는 식이 0이 되는 값을 찾으면 그게 바로, x축, y축으로 이동하는 개념이 됩니다. 즉, x-m =0, y-n=0을 계산하면 x=m, y=n이 되는 것이지요. 즉 서로 이동한 만큼의 반대 부호를 대입해 주면 된다는 것을 보여줍니다.
∎ 함수의 대칭
어떤 함수가 특정 조건에서 대칭을 이룰 때, 원점에 대칭이면 홀함수 또는 기함수(odd function)라고 하고, y축 대칭 함수를 짝함수 또는 우함수(even function)라고 하며, 이것을 정리하면 다음과 같습니다.

∎ 다항 함수의 기함수와 우함수
지수가 짝수 항과 상수항으로만 이루어진 함수는 우함수이고, 지수가 홀수 항으로만 이루어진 함수는 기함수가 됩니다.
∎ 삼차함수가 변곡점에서 대칭인 이유 증명
1. 다음과 같은 삼차함수가 있습니다.

2. 이 함수를 두 번 미분한 것이 0인 x값을 찾습니다.

3. f(x)의 변곡점은 x 대신에 2에서 구한 x값을 대입하면 다음과 같이 정리할 수 있습니다.

4. 이제 3에서 구한 변곡점이 원점(0, 0)이 되도록 평행이동 시켜 보겠습니다. 이동시킨 함수는 f(x) 함수와 다르므로 g(x)라고 하고, 위에서 언급한 함수의 평행이동 개념을 이용하면 다음과 같이 정리할 수 있습니다. 즉, f(x)의 변곡점을 아래와 같이 평행이동시키면, g(x)의 변곡점은 원점이 되며, 다음과 같이 표현할 수 있겠습니다.

5. f(x-b/3a) 값을 계산해서 g(x) 값을 정리하면 다음과 같습니다.
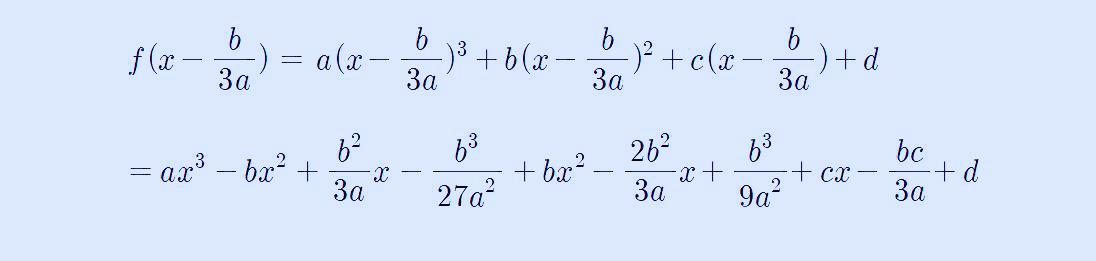
6. g(x)는 다음과 같이 정리할 수 있습니다.

7. 위에서 밝힌 것처럼 지수가 지수가 홀수 항으로만 이루어진 함수는 기함수(홀함수)이므로 g(x)는 기함수가 되며, 홀함수는 원점에서 대칭이므로 삼차함수는 변곡점에서 대칭된다고 할 수 있습니다.
8. 이상으로 3차 함수가 변곡점에서 대칭되는 이유에 관해서 살펴보았습니다.
'수학 이야기' 카테고리의 다른 글
| 2022 수능 생명과학2 오류 논란을 보면서 (2) | 2021.12.12 |
|---|---|
| 삼차함수 비율 관계를 증명해 보자 (0) | 2021.12.04 |
| 2022 수능 수학 1번, 난감했다고 한다 (0) | 2021.11.28 |
| 삼차함수 극대 극소 차 공식 (1) | 2021.11.23 |
| 아름다운 3차 함수 비율 관계와 3차 함수 그래프 개형 (0) | 2021.11.21 |






