삼차함수 계수 부호 결정하기
삼차 함수 계수의 부호를 결정하는 방법에 관해서 알아봅시다.
삼차 함수 계수의 부호를 알아보기 위해서는 이차함수 계수의 부호를 아는 방법을 미리 살펴보는 것을 추천드립니다. 다음 글을 참고해 보세요.
https://nous-temperature.tistory.com/367
이차함수 그래프 계수 부호 구하기
수학 시험에서 모든 문제가 답을 구하는 데 5분 또는 10분이 걸리지 않을 것입니다. 일부 문제는 빠르게 구하여 시간을 확보하는 것이 필요할 수 있습니다. 계산하는 데 절대 시간이 필요한 문제
nous-temperature.tistory.com
예시를 들어서 먼저, 살펴보도록 하겠습니다.
다음과 같은 삼차 함수가 있고, 그래프가 다음과 같을 때, 계수의 부호를 결정하는 방법입니다.
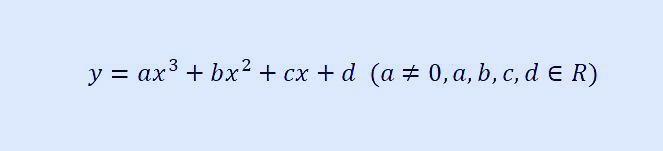
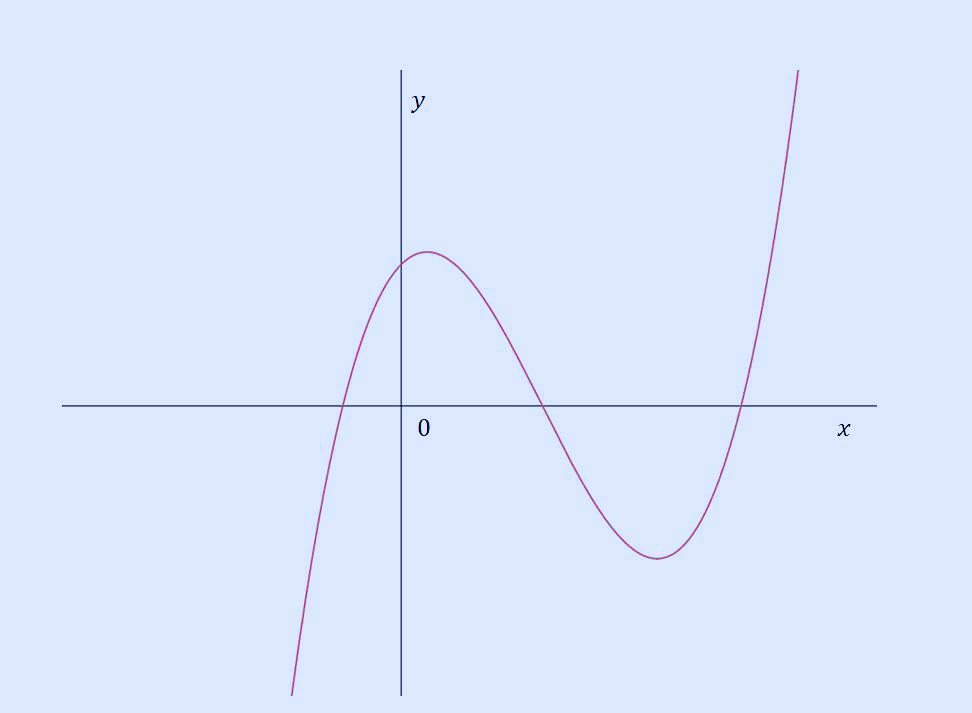
위 삼차 함수를 보면, 먼저, 왼쪽 부분 아래에서 오른쪽 부분으로 위로 올라가는 형태의 그래프이므로 a는 양수가 됩니다. 또한, d는 y 절편(삼차 함수에서 x가 0 인 값, 또는 삼차 함수와 y축이 만나는 점)이고, 이 값이 위 그래프에서 0보다 위에 있는 점이므로 d는 양수입니다. 삼차 함수의 특징을 어느 정도 익힌 수험생이라면 a와 d의 부호는 그래프만 보아도 바로 알 수 있을 것입니다.
이제 c의 부호를 결정할 때입니다. c의 부호는 삼차 함수와 y축에서 만나는 점(=d)에서의 접선의 기울기와 같은 의미가 됩니다. 따라서, 아래처럼 c의 부호는 d에서 접선을 그으면 다음과 같은 모습이 됩니다.

위 그래프에서 파란색 선이 d에서 접선이고, 이 직선의 기울기가 양수이므로 c도 0보다 큰 양수가 됩니다.
이제 b의 계수의 부호만 남았네요. 먼저, b의 부호를 알려면, 위 그래프에서 극댓값과 극솟값을 가지므로 그 값을 알파와 베타로 본다면 다음과 같이 쓸 수 있습니다.

위 그래프에서 극댓값과 극솟값의 x 좌표는 모두 양수이므로 알파와 베타의 합은 0보다 큰 값이 되므로 양수가 됩니다. 따라서 삼차 함수를 한번 미분한 값에서 두 근의 합이 양수라고 할 수 있습니다. 식으로 쓰면 다음과 같겠네요.

위 마지막 식에서 a는 양수이므로 -2b가 0보다 크려면, b는 음수, 즉 0보다 작아야 합니다. 이렇게 삼차 함수 계수의 부호를 모두 결정했습니다.

그런데 말이죠. 왼팔을 이용한 이차함수 계수의 부호를 결정할 때처럼 b의 부호는 좀 더 간단하게 구할 수 있을지도 모릅니다.
삼차 함수와 한번 미분한 값을 0이라고 한다면, x가 알파와 베타일 때 극댓값, 극솟값을 가지므로 이를 그래프로 나타내면 다음과 같습니다.
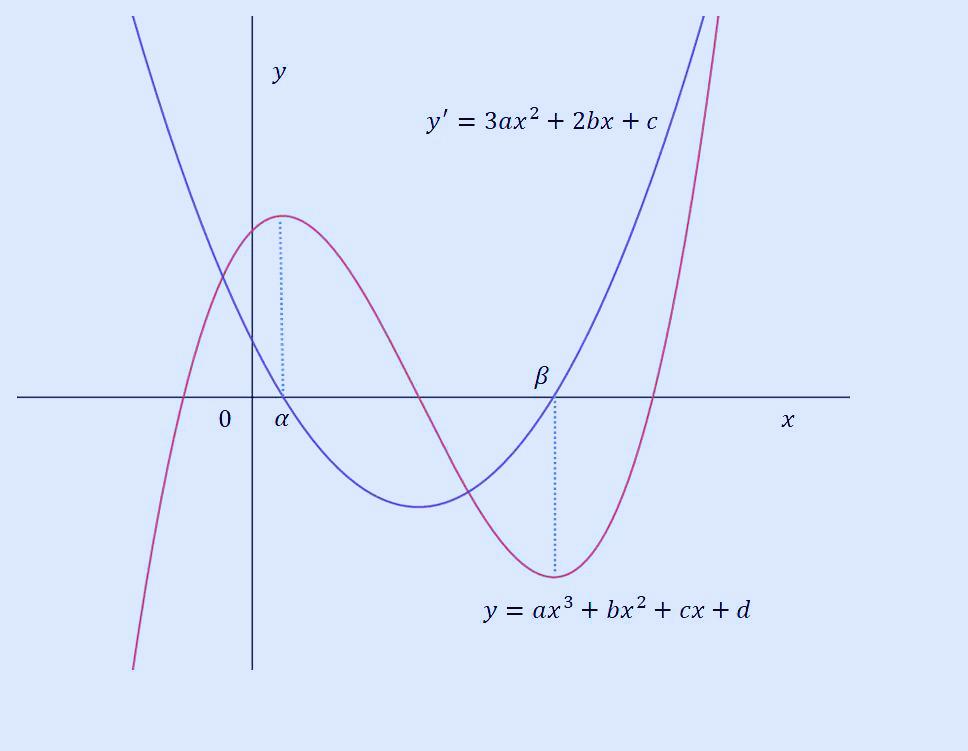
삼차식을 한번 미분한 값이 위의 파란색 이차식 그래프가 되었고, 이 이차식에서 2b는 x 계수이고, b의 부호는 2차식에서 x 계수의 부호이므로 이는 결국 이차식의 y절편에서 접선의 기울기의 부호와 같은 것이 됩니다. 다음과 같이 말이죠.

즉, b의 부호는 위 그래프에서 녹색 직선의 기울기의 부호와 같기 때문에 b는 음수가 되겠습니다.
몇 번만 규칙을 익히면, 삼차 함수 계수의 부호는 눈으로만 보아도 알 수 있을 듯합니다. b의 계수가 0, c의 계수가 0, d의 계수가 0인 것도 어렵지 않게 판별할 수 있겠네요.
이상으로 삼차 함수 계수의 부호를 눈으로만, 아니 두 팔을 이용해서, 그게 아니면 하나씩 계산해서 결정하는 방법을 알아보았습니다.
'수학 이야기' 카테고리의 다른 글
| 루트 2 무리수 증명 (0) | 2022.03.17 |
|---|---|
| 한평 크기, 면적은 길이가 몇 미터? 루트 2 값 계산으로 알아보기 (1) | 2022.03.16 |
| 삼차함수 1대 루트3 증명 (0) | 2022.03.05 |
| sin15 도, cos15 도, tan15 도 값 알아보기 (0) | 2022.02.26 |
| 2022 수능 생명과학2 오류 논란을 보면서 (2) | 2021.12.12 |






