점과 직선 사이의 거리 공식 증명
점(x1, y1)과 직선(ax+by+c=0)까지 가장 짧은 거리(d) 공식은 보통 다음과 같이 정리할 수 있습니다.

여러 가지 방법이 있지만, 이 공식이 어떻게 나왔는지 고등학교 1학년 수학 수준에서 공식을 증명해 보도록 하겠습니다.
좌표 평면 위의 한 점 A(x1, y1)와 직선 ax+by+c=0이 있다고 할 때, 점 A와 직선까지의 최단 거리는 점 A에서 직선에 수직선을 내렸을 때, 그 직선 위의 점 B(x2, y2)까지의 거리라고 할 수 있습니다.

위 그래프에서 선분 AB의 기울기는 다음과 같습니다. 직선의 기울기는 x의 증가량 분의 y의 증가량이기 때문이죠.
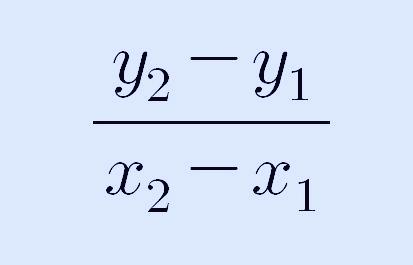
직선 ax+by+c=0의 기울기는 다음과 같이 쓸 수 있습니다.

두 직선이 수직으로 만날 때, 두 직선의 기울기 곱은 -1이 되어야 하므로 다음과 같이 쓸 수 있습니다.
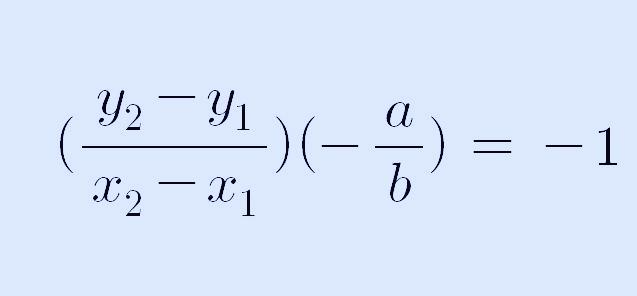
위 식을 더 계산해서 정리하면 다음과 같습니다.
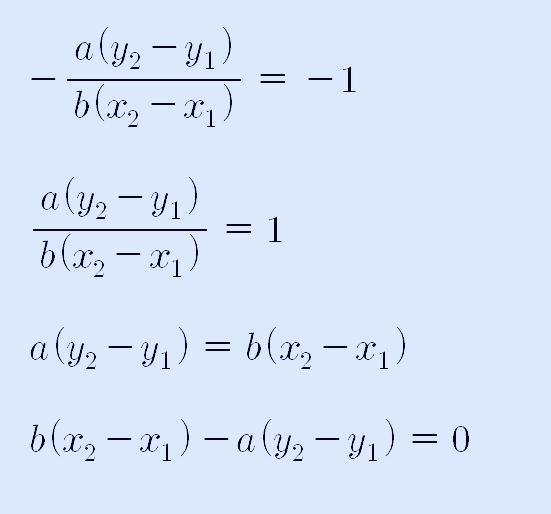
또한, 점 B(x2, y2)는 직선 ax+by+c =0 위의 점이므로, x = x2, y=y2을 대입해도 성립해야 하므로 다음과 같이 쓸 수 있습니다.


위 식을 약간 변형해 보겠습니다. 앞에서 두 직선이 수직일 때, 기울기의 관계식에 a(x2-x1), b(y2-y1)이 있으므로 이것이 나오도록 변형하는 것입니다. 다음과 같이 같은 수를 더해주고 빼주면서요.

위 식을 a와 b로 묶어서 정리하면 다음과 같습니다.

위 계산식과 앞서 구한 식을 연립해서 x2-x1, y2-y1의 값을 구해 줍니다.
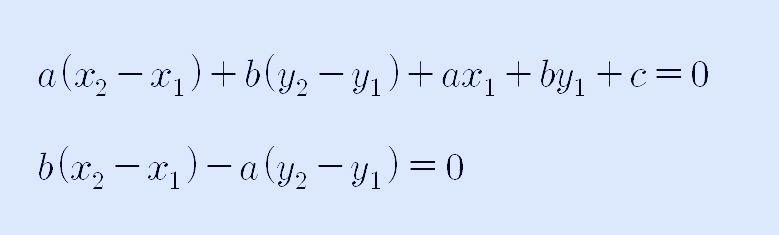
x2-x1을 구하기 위해, 아래 식에 b/a를 곱하고 위의 식과 더해 줍니다.

y2-y1을 구하기 위해, 위의 식에 b/a를 곱하고 두 식을 빼줍니다.
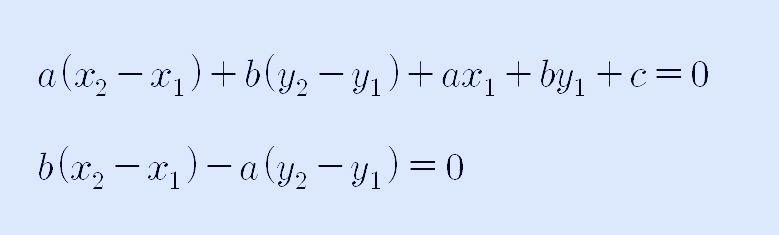
그러면 다음과 같은 식이 나옵니다.

정리하면 다음과 같습니다.

그래프에서 선분 AB의 길이는 직각삼각형의 빗변의 길이이므로 이 빗변을 d라고 하면 피타고라스 정리에 의해서 다음과 같이 쓸 수 있습니다.

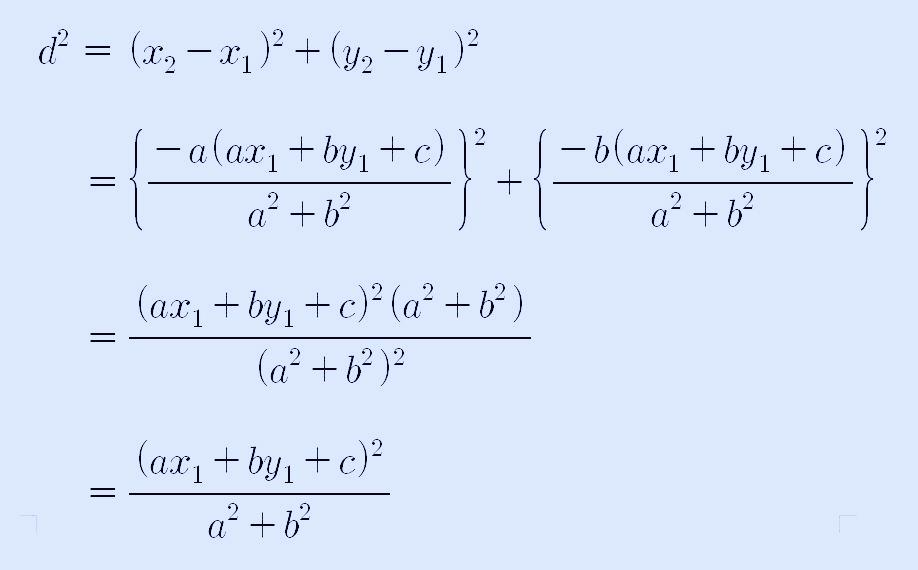
따라서, d는 다음과 같이 정리할 수 있습니다.

이상으로 점과 직선 사이의 거리 공식에 관해서 알아보았습니다.
'수학 이야기' 카테고리의 다른 글
| 2023 6월 모의고사 수학 15번 고3, 등차 수열의 점화식 이해 (1) | 2022.06.11 |
|---|---|
| 2023 6월 모의고사 수학 22번 풀이 - 함수의 극한과 연속 (1) | 2022.06.10 |
| 자연상수 e, 무리수 e 계산 해 보기 (1) | 2022.05.28 |
| 쌀 한 톨의 무게와 제곱수의 위력 (4) | 2022.05.24 |
| 루트3 근사값 계산법과 무리수 증명 하기 (0) | 2022.03.20 |






