2023 6월 모의고사 수학 22번 풀이 - 함수의 극한과 연속
2022년 6월 9일에 실시된 한국교육과정평가원 수능 모의고사 수학 22번 풀이입니다.
교육부에서는 6월 모의평가 영역별 출제 방향을 제시했는데, 이 문제는 다음과 같이 언급하고 있습니다.
"수학 II에서는 함수의 극한과 연속함수의 성질을 활용하여 문제를 해결할 수 있는지를 묻는 문항(22번)"
이 언급에서 함수의 극한과 연속함수의 성질을 먼저 알아보고자 합니다.
대부분의 교과서에서 다음과 같이 함수 극한에 관한 성질을 언급하면서, 0/0 꼴이면서 근호가 있는 함수의 극한값을 어떻게 구하는지를 말해주고 있습니다.

위 설명에서 6월 모의고사 22번은 아래 주어진 식을 푸는 하나의 실마리를 제시해 줍니다. 처음 보았을 때는, 매우 복잡한 식일 수 있는데, 아래 식에서 g(t)는 상수이므로 신경 쓰지 말고 "근호가 들어 있는 부분의 유리화"라는 개념을 이용하여 주어진 식을 유리화합니다.
즉, 주어진 식은 분자에 근호가 있고, 상수 g(t)가 있으므로 분자와 분모에 다음과 같이 동일한 식을 써주면 됩니다.

위 식에서 분자는 (a+b)(a-b)=a2 - b2의 형태가 되므로 분자의 근호가 없어지고, 다음과 같이 쓸 수 있습니다.
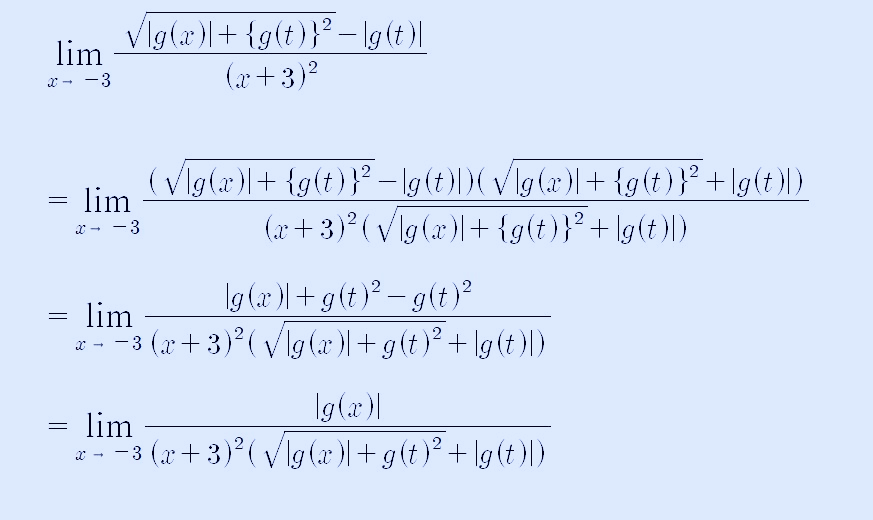
이렇게 계산해 놓고 보니, x가 -3으로 가면 (x+3)2이 0으로 가므로, |g(x)|는 (x+3)2을 인수를 가져야 합니다. 맨 처음 주어진 식에서 x <0에서 g(x)는 (x+3)f(x)이므로 f(x)는 (x+3)을 인수로 가져야 하고, f(x)가 이차식이라고 했으므로 f(x)는 다음과 같이 쓸 수 있습니다.
f(x) = (x+3)(x-p)
따라서, g(x)는 x<0에서 다음과 같이 쓸 수 있습니다.
g(x) = (x+3)(x+3)(x-p)
이 g(x) 값을 극한값 마지막에 정리한 식에 대입합니다.

여기까지 계산하고 보니, 분자와 분모에 (x+3)은 약분이 되고 다음과 정리됩니다.
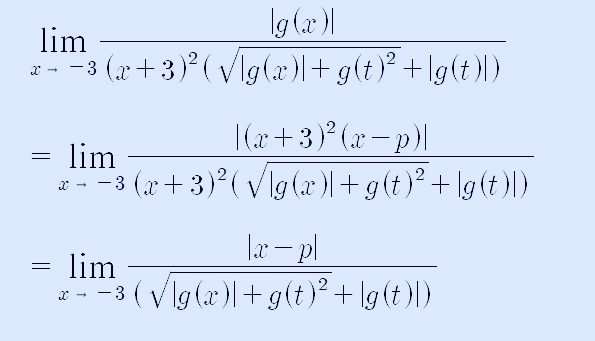
x <0에서 g(x)= (x+3)f(x)이 주어졌으므로, x=-3을 대입하면, g(-3) = 0이 됩니다.
따라서, x가 -3으로 갈 때, |g(-3)|= 0이므로, 아래 식을 계속 풀면 극한값은 아래와 같이 정리할 수 있습니다.

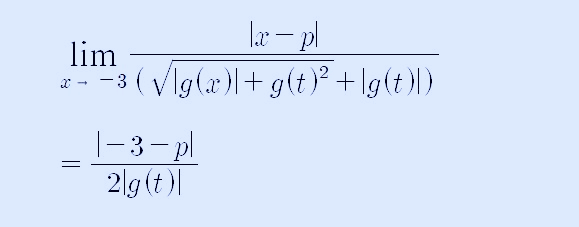
그런데, 이 극한값이 존재하지 않기 위해서는 분모의 값이 0이 되어야 하고, t의 값이 -3과 6 뿐이라고 했으므로, g(-3)=0, g(6)=0이 되어야 합니다.
이제 문제에서 f(x) = (x+3)(x-p)이므로 f(x-b)=(x-b+3)(x-b-p)입니다. 따라서 맨 앞에 주어진 g(x)를 다시 정리해 보겠습니다.
g(x) = (x+3)(x+3)(x-p) (x<0)
=(x+a)f(x-b) = (x+a)(x-b+3)(x-b-p) (x≥0)
이제 함수의 연속에 관해서 생각해 봅니다. 대부분의 교과서에 어떤 함수가 실수 a에 대하여 연속일 때, 다음 3 조건을 만족해야 한다고 표현하고 있습니다.

문제의 조건에서 g(x)는 모든 실수에서 연속이라고 했으므로, 위의 조건에 적용시켜보면, g(x) = (x+3)(x+3)(x-p) (x<0)에서 g(-3)=0이 되고, x가 -3으로 갈 때, 극한값 g(-3)=0이므로 x=-3에서 연속이 됩니다. 그런데, x-p의 값도 0이 될 수 있으므로, p=-3이면 x=-3을 대입했을 때, g(-3)=0이 되므로 연속이 됩니다. 그런데, p의 값이 -1이라고 가정하면, x=-1에서 g(x)=0이 되므로 g(-3)=0, g(6)=0 뿐이라는 조건에 위배됩니다. 따라서 p=-3이 되어야 합니다.
x≥0 범위 g(x)=(x+a)f(x-b) = (x+a)(x-b+3)(x-b-p)에서 g(6)=0이므로 g(6) = (6+a)(6-b+3)(6-b-p) = 0이 되어야 합니다. a가 양수라는 조건이 있으므로 6+a는 0이 될 수 없고, 6-b+3=0 또는 6-b-p=0이 되어야 합니다. 결국엔 두 식이 같아야 성립하겠네요.
따라서 b=9가 되고, p=-3이 됩니다. 이 값을 g(x)로 정리하면 다음과 같습니다.
g(x) = (x+3)(x+3)(x+3) (x<0)
=(x+a)f(x-9) = (x+a)(x-9+3)(x-9+3) (x≥0)
g(x)가 0에서 연속이 되려면, x가 0으로 갈 때, 극한값과 g(0)의 값이 같아야 하므로 다음과 같이 정리할 수 있습니다.
33=a(0-6)(0-6)
27=36a
a = 27/36 = 3/4
이제 구하고자 하는 g(4)의 값은 문제의 정답은 g(x) = (x+a)(x-9+3)(x-9+3) (x≥0) 식에 x=4, a=3/4를 대입하면 나옵니다.
15번 문제 해설은 다음 글에 있습니다.
https://nous-temperature.tistory.com/671
2023 6월 모의고사 수학 15번 고3, 등차 수열의 점화식 이해
2022년 6월 9일 실시된 2023학년도 한국교육과정평가원 주관 고3 6월 모의고사 수학 15번 풀이법을 소개합니다. 문제에서 다음과 같은 수열이 제시되어 있습니다. 조건은 k는 자연수, a1= 0, a22=0가 되
nous-temperature.tistory.com
조금은 도움이 되었으면 합니다.
'수학 이야기' 카테고리의 다른 글
| 계차수열이란? 계차수열 일반항 공식 구하기 (0) | 2022.06.12 |
|---|---|
| 2023 6월 모의고사 수학 15번 고3, 등차 수열의 점화식 이해 (1) | 2022.06.11 |
| 점과 직선 사이의 거리 공식 증명 (3) | 2022.06.03 |
| 자연상수 e, 무리수 e 계산 해 보기 (1) | 2022.05.28 |
| 쌀 한 톨의 무게와 제곱수의 위력 (4) | 2022.05.24 |






