계차수열이란? 계차수열 일반항 공식 구하기
오랫동안 잊어버리고 있었던 저의 블로그 글이 하나 있습니다. 2년 전쯤에 썼던 점화식에 관한 글인데요. 그 글에서 계차수열 언급을 잠깐 했습니다. 계차수열은 2007 개정 교육과정까지 수학에 적용되는 개념이었지만, 2012년 이후에 적용된 2009 개정 교육과정과 2015 개정 교육과정에서는 명시적으로 계차수열은 포함하지 않는다고 언급하고 있습니다. 즉, 현재부터 2028학년도 수능까지는 교육과정이 바뀌지 않는 이상 계차수열이 시험에 나올 수 없다는 것입니다.
그래서 2년 전에 썼던 그 글은 교육과정에 나오지 않은 개념을 포스팅하는 것이 마땅치 않아서 그 후로 까맣게 잊고 있었던 것 같습니다.
그런데 말이죠.
왜 계차수열에 관한 검색은 그리도 많이 하는 것일까요? 계차수열을 검색하는 사람은 일반인이지 않을 거란 생각을 합니다. 대부분 고등학교 2학년 이상의 학생들일 텐데, 왜 검색하는 것일까요?
게다가 계차수열의 개념을 알아야 이해할 수 있는 수열의 점화식의 일반항을 구하는 문제 중에서, 그 풀이 과정을 한 번도 접하지 못한 학생들은 손도 대지 못할 그 문제가 왜 끊임없이 소개되는지 이해할 수 없어서 자료를 조금 찾아보았습니다.
그랬더니, 대학 입학시험에서 면접으로 합격할 수 있는 수학 면접이 었더군요. 정확하게 언제인지는 모르지만, 이 계차수열의 개념을 알아야 이해할 수 있는 수열의 점화식 문제가 수학 면접 예시 문항으로 나온 것을 보았습니다. 아마도 2012년 이전의 수학 면접 문제 예시라고는 생각 들지만, 아직도 수학 면접을 준비하는 수험생 입장에서는 이것을 아직도 무시하지 못하고 있지 않을까 생각합니다.
행렬이 일반 수학I, 수학II에서 없어진 지 꽤 오래되었지만, 전문 교과목인 고급수학에 언급되었기에 뭐 응용해서 나올 수 있다곤 치더라도, 계차수열 응용문제는 참으로 이해되지 않은 것 중의 하나입니다. 교육과정을 벗어난 수학의 개념을 이용해서 문제를 해결하라니....
그냥 넘어갈까 하다가, 정말 정말 그러지 않기를 바라지만, 혹시나 하는 마음에 계차수열의 개념과 일반항 구하는 방법에 관해서 설명해 볼까 합니다. 이 글이 정말 고등학교 학생들에게는 쓸모없기를 기대하면서 말이죠.
다음과 같은 수열이 있습니다.
1, 3, 10, 22, 39, ....와 같은 수열이 있습니다.
이 수열은 교육과정에 포함된 등차수열이 아닙니다. 왜냐하면, 첫 번째 숫자에 차례대로 일정한 수를 더한 수열을 등차수열이라고하는데, 2은 1에 2를 더한 수이고, 10은 2에 7을 더한 수이고, 22는 10에 12를 더한 수이기 때문에 일정하지가 않습니다. 뭐, 정의에 따라 그렇다는 것입니다.
첫 번째 숫자에 차례로 일정한 곱해서 얻은 수열을 등비수열이라고 하기 때문에 위 수열은 등비수열도 아닙니다.
1, 3, 10, 22, 39, ....
이 수열을 자세히 보면, 3에서 1을 빼면 2가 되고, 10에서 3을 빼면 5가 되고, 22에서 10을 빼면 12가 되고, 39에서 22를 빼면 17이 됩니다. 이렇게 뺀 수를 정리하면 다음과 같습니다.
2, 7, 12, 17, ....
위 수열은 규칙이 보이나요?
그렇습니다. 이렇게 하면, 2에 5를 더하면 7이 되고, 7에 5를 더하면 12가 되고, 12에 5를 더하면 17이 됩니다. 즉, 이 수열은 등차수열의 정의, "첫 번째 항부터 일정한 수를 차례로 더한 수열"이 됩니다.
이렇게 어떤 수열에서 인접한 두 항의 차로 이루어진 수열을 "계차수열"이라고 합니다. 일반항을 찾기 위해서 다음과 같이 두 수열의 특징을 다음과 같이 다시 써 보겠습니다.
1, 3, 10, 22, 39, ....
2, 7, 12, 17, ....
위에 있는 수열은 원래 수열, 밑에 있는 수열 앞에 있는 항과 뒤에 있는 항의 차이를 쓴 것입니다. 3은 1에 2를 더한 것이고, 10은 1에 2를 더하고 7을 더한 것이며, 22는 1에 2, 7, 12를 더한 것이며, 39는 1에 2, 7, 12, 17을 더한 것입니다.
1, 3, 10, 22, 39,....로 이루어진 수열을 an이라고 하고, 2, 7, 12, 17, ....로 이루어진 수열을 bn이라고 한다면,
a1 = 1
a2= a1 + b1 = 1+2
a3 = a1 + b1 + b2 =1+2+7
a4 = a1 + b1 + b2 + b3 = 1+2+7+12
a5 = a1 + b1 + b2 + b3 + b4 = 1+2+7+12+17
.........
an = a1 + b1 + b2 + b3 + b4 + .... + bn-1 이 됩니다.
위의 a의 n번째 항을 이제 시그마 기호를 써서 나타내 보겠습니다.
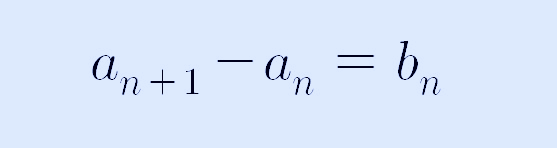

위 식은 나중에 포스팅할 수열의 점화식을 해결하는 데 강력한 개념이 될 수 있습니다.
이제 bn, 즉, 2, 7, 12, 17, ....의 일반항을 구해 봐야겠습니다. 2, 7, 12, 17, ....은 공차가 5인 등차수열입니다.
이 등차수열의 일반항을 구하는 것은 교육과정에 기본적인 개념으로 나와있으므로 어렵지 않게 다음 공식에 대입하면 일반항을 구할 수 있을 겁니다.
bn=a + (n-1)d (n =1, 2, 3, ....)
a=2, d=5
bn=2+(n-1)x5 = 5n-3
따라서, 계차수열의 일반항 구하는 공식에 bn = 5n-3을 대입하면, 1, 3, 10, 22, 39, ....의 일반항을 구할 수 있겠네요.

위 식을 계산하면 계차수열의 일반항을 구할 수 있겠습니다.
'수학 이야기' 카테고리의 다른 글
| 수열의 귀납적 정의, 동차 선형 점화식 일반항 구하기 (1) | 2022.06.17 |
|---|---|
| 삼각함수 실생활 활용 사례 (1) | 2022.06.16 |
| 2023 6월 모의고사 수학 15번 고3, 등차 수열의 점화식 이해 (1) | 2022.06.11 |
| 2023 6월 모의고사 수학 22번 풀이 - 함수의 극한과 연속 (1) | 2022.06.10 |
| 점과 직선 사이의 거리 공식 증명 (3) | 2022.06.03 |






