수열의 귀납적 정의, 동차 선형 점화식 일반항 구하기
이 글은 수능 대비용이 아닙니다. 2015 수학 교육과정에 포함되지 않은 것으로 판단되기에 수능을 준비하는 수험생을 위한 글이 아님을 밝힙니다. 그저 수열의 귀납적 정의를 공부하다 보면 접하게 되는 문제일 수 있기에 이를 정리하는 입장에서 쓰는 글로 이해하시면 되겠습니다. 다음과 같은 3가지의 수열의 일반항을 구하는 문제를 해결하는 방법입니다.

위와 같은 수열은 동차 선형 점화식이라는 어려운 용어로 일컬어지며, 1번째 수열은 수능을 준비하는 수험생들이 한 번쯤 보았을 문제로 파악됩니다. 1번 문제를 확장하여 3번 유형의 문제까지 공부하는 경우도 있는 것 같지만, 이전 계차수열 포스팅에서 밝힌 것처럼 이 문제는 현재 교육과정에 적용할 수 없는 문제라고 생각합니다. 따라서, 이 문제를 공부하는 것은 수능을 준비하는 입장에서는 개인의 선택이라고 봅니다. 어찌 되었든 간에, 이 문제 유형에서 3번째 문제를 해결하는 방법을 먼저 알아볼까 합니다. 보통 순차적으로 1~3번 문항 순서로 설명하는 경우가 많지만, 더 어려운 3번째 방법을 알면 1, 2번도 쉽게 이해되리라 보기 때문입니다. 3번 문제는 보통 다음과 같은 형식을 가지는 수열입니다.

위 식에서 p가 0이 아니므로 p로 양변을 나누면 다음과 같이 계산할 수 있습니다.

여기에서 이차방정식의 근과 계수의 관계를 생각해 보도록 하겠습니다. 아래처럼 두 근의 합과 곱으로 이루어진 이차방정식이 정리되는 방식은 다음과 같습니다.


이렇게 쓰고 보니, 문자만 다를 뿐 수열은 이차방정식의 근과 계수의 관계와 동일한 형태가 되었습니다. 따라서, 이 수열을 이차방정식으로 a의 n+2를 이차, n+1일 1차, n을 상수로 두고, 그 근을 알파와 베타라고 한다면, 주어진 수열은 다음과 같이 쓸 수 있습니다.

이렇게 정리된 수열을 전개를 해 보겠습니다.

위와 같이 정리된 식은 다음 두 가지 방법으로 정리할 수 있습니다.

①, ②번 수열을 자세히 보면 α와 β로 정리된 수열이 되는데, ①번 수열에서 an+1 - αan = bn 하고, an+1 - βan = cn이라고 하면 각각의 수열은 공비가 β와 α인 공비 수열이 됩니다. 다음과 같이 말이죠.
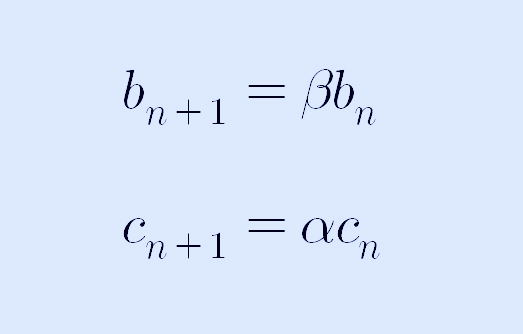
따라서 각 수열의 일반항은 다음과 같이 쓸 수 있습니다.

an+1 - αan = bn, an+1 - βan = cn이므로 이로 다시 정리하면 위 식은 다음과 같이 쓸 수 있습니다. a2 - αa1 = b1, a2 - βa1 = c1이므로,
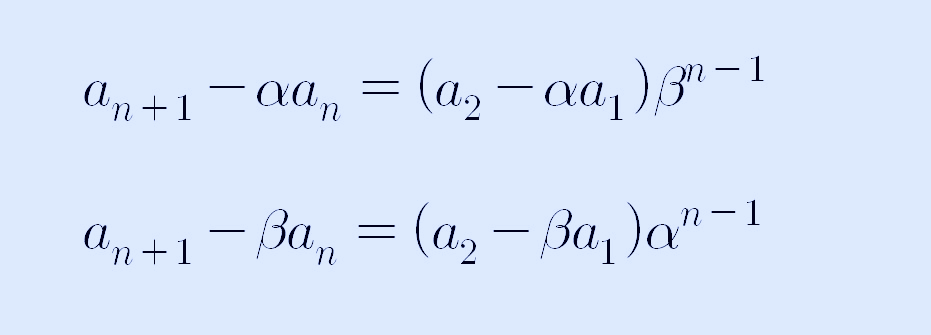
로 쓸 수 있습니다. 위 두 식을 빼면, an+1은 제거되고 다음과 같은 수열의 일반항이 구해집니다.

β-α이 0이 아니라고 하면 양변을 이것으로 나누면 구하고자 하는 최종 an이 다음과 같습니다. 맨 처음 주어진 문제에서 두 근을 빼면 0이 되는 꼴은 나중에 해결하도록 하겠습니다.
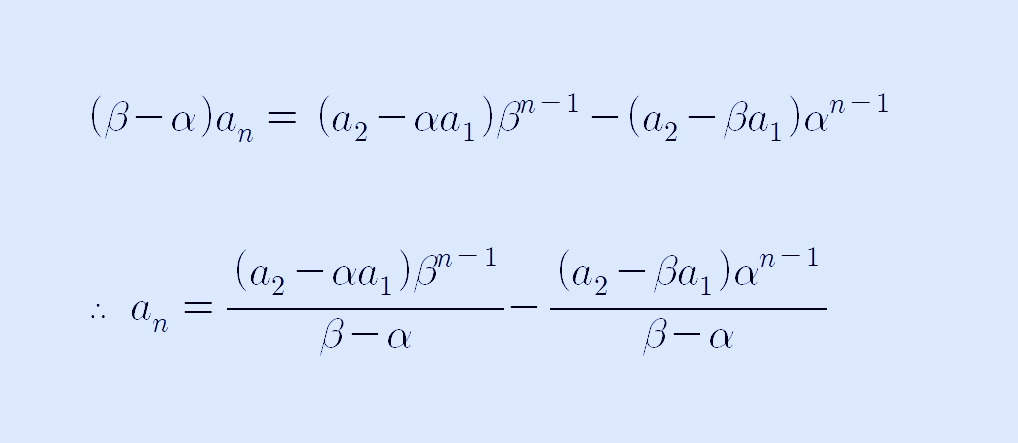
이런 방식으로 풀면, 맨 처음 제시한 3번째 문제도 해결할 수 있겠습니다.

위 식에서는 알파와 베타가 -3, 2이므로 이 수를 대입하면 수열의 일반항을 구할 수 있습니다.
또한, 맨 처음 제시한 문제에서 1번과 2번 문제는 3번 문제보다 약간 더 쉽게 해결할 수 있을지도 모릅니다. 이 설명은 다음 기회로 미루며, 오늘은 여기까지입니다.
'수학 이야기' 카테고리의 다른 글
| 피보나치수열의 일반항 구하기 (0) | 2022.07.12 |
|---|---|
| 이차함수 실생활 활용 사례 - 자동차 안전거리 공식 (3) | 2022.06.22 |
| 삼각함수 실생활 활용 사례 (1) | 2022.06.16 |
| 계차수열이란? 계차수열 일반항 공식 구하기 (0) | 2022.06.12 |
| 2023 6월 모의고사 수학 15번 고3, 등차 수열의 점화식 이해 (1) | 2022.06.11 |






