피보나치수열의 일반항 구하기
피보나치 수열이라는 재미있는 수열이 있습니다.
관련 포스팅을 한 적이 있는데 이번 시간에는 피보나치수열의 특징이 아닌 일반항을 구해보도록 하겠습니다.
먼저, 피보나치 수열이 무엇인지 잠시 다시 한번 언급해 보도록 하겠습니다.
1, 1, 2, 3, 5, 8, 13, 21,...처럼 이루어진 수열을 말합니다.
이 수열을 자세히 보면, 뒤에 있는 항은 바로 앞에 있는 두 개의 항의 합으로 이루어져 있습니다. 이전 관련 포스팅에서 언급한 것처럼 가장 자연적인 수열이라고 할 수 있습니다.
이 수열의 일반항은 어떻게 구할까요?
21은 앞에 나온 8과 13을 더해서 나온 수인데, 이를 하나의 문자 식으로 쓰면 첫 번째 앞에 있는 항을 an이라고 하면, 두 번째 항은 an+1이 되고, 세 번째 항은 an+2라고 할 수 있는데, an+2 = an+1 + an으로 나타낼 수 있습니다.
어디서 많이 본 수열처럼 보이지 않나요? 오른쪽에 두 개의 항을 왼쪽으로 이항을 하면 다음과 같습니다.
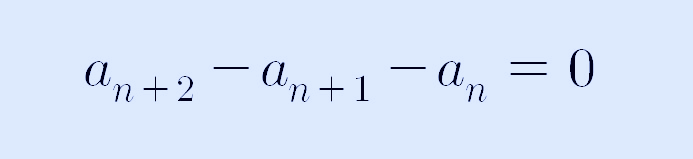
맞습니다. 며칠 전에 썼던 저의 아래 글을 참고하면, 앞에 숫자만 다른 p+q+r ≠ 0인 수열이 되었습니다.
https://nous-temperature.tistory.com/674
수열의 귀납적 정의, 동차 선형 점화식 일반항 구하기
이 글은 수능 대비용이 아닙니다. 2015 수학 교육과정에 포함되지 않은 것으로 판단되기에 수능을 준비하는 수험생을 위한 글이 아님을 밝힙니다. 그저 수열의 귀납적 정의를 공부하다 보면 접하
nous-temperature.tistory.com
피보나치수열은 첫 번째 항은 1, 두 번째 항이 1이고, 위에서 제시한 식을 2차 방정식이라고 하면, 두 근은 다음과 같이 계산할 수 있습니다.

한 근을 알파라고 하고, 다른 근을 베타라고 한다면, 알파와 베타는 다음과 같이 쓸 수 있겠네요.
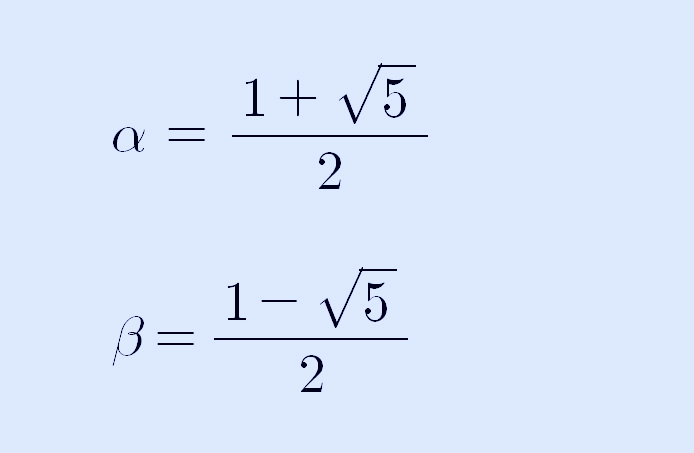
이전 "수열이 귀납적 정의, 동차 선형 점화식 일반항 구하기" 글에서 두 근이 알파와 베타라고 했을 때 일반항은 다음과 같다고 계산했었습니다.

위 식의 알파와 베타에 앞에서 계산한 알파와 베타를 넣어서 계산하면 다음과 같이 정리할 수 있겠네요.

매우 복잡한 식이 나왔지만, 조금 인내를 가지고 하나씩 계산해 보도록 하겠습니다. 아래처럼 계산하니 조금씩 규칙성이 보이기 시작하는 듯합니다.

분자를 최대한 간단하게 더 계산해 보겠습니다.

이제 거의다 계산이 끝나 갑니다. 조금만 더 힘을 내 보자고요.

가장 자연을 닮았다고 하는 피보나치수열의 일반항은 다음과 같습니다.

아직 수열 관련해서 포스팅할 게 있습니다. p+q+r=0인 수열의 일반항 풀이가 며칠 이내에 곧 이어질 예정입니다.
'수학 이야기' 카테고리의 다른 글
| 근의 공식 유도, 그리고 이차방정식 판별식 (0) | 2022.07.20 |
|---|---|
| 이상한 나라의 수학자, 리만 가설, 파이송 (1) | 2022.07.17 |
| 이차함수 실생활 활용 사례 - 자동차 안전거리 공식 (3) | 2022.06.22 |
| 수열의 귀납적 정의, 동차 선형 점화식 일반항 구하기 (1) | 2022.06.17 |
| 삼각함수 실생활 활용 사례 (1) | 2022.06.16 |






