원주율 구하기, 3.14 구하는 방법, 파이 구하는 공식에 대해 알아보자
원주율(파이: π)은 원의 지름에 대한 원둘레의 비율을 말하며, 보통 3.14...정도로 알려져 있습니다. 어떤 원이든지 원의 둘레의 길이는 원 지름 길이의 약 3.14배가 된다는 말이죠.
이 3.14...를 구하는 방법은 여러 가지가 있지만, 이 글에서는 고등학교 때 배우는 "이항정리", "적분"의 개념과 그 이전에 배웠을 원의 넓이 구하는 방법을 통해서 알아보고자 합니다.
먼저, 이항정리는 다음과 같이 정리됩니다.
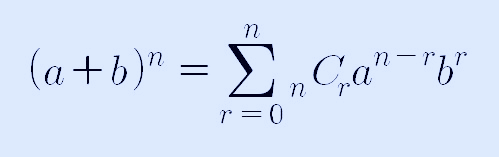
위 이항정리에서 a=1, b=x를 대입하면 다음과 같이 정리할 수 있습니다.
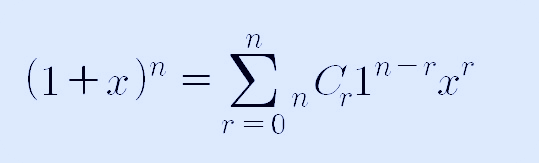
위 식을 전개하면 다음과 같습니다.

위 식에서 C의 값을 숫자와 n으로 계산해서 정리하면 아래와 같습니다.

이제 n을 1/2이라고 가정해 보겠습니다. 왜 그 많은 수 중에서 2 분의 1인가는 원의 방정식 때문입니다.

위 원의 방정식의 중심이 원점(0, 0)이고 반지름이 1인 원의 방정식은 다음과 같으며, 이 방정식을 y에 대해서 정리하면 다음과 같습니다.

원의 방정식을 y에 대해서 정리했더니 지수가 1/2이 되었기 때문에 위의 이항정리 전개식에서 n을 1/2로 정하고 전개해서 정리하면 다음과 같게 됩니다.

왼쪽 식과 바로 위의 원의 방정식에서 도출한 y의 값과 비슷하게 되었네요. 이제 x 대신에 -x 제곱으로 두고 정리하면 다음과 같습니다.

아래 원의 방정식에서 원점이 중심이고 반지름이 1인 원의 넓이는 파이가 되고, 색칠한 부분의 넓이는 원의 넓이 4 부분 중의 하나이므로 4분의 파이가 됩니다.

따라서 마지막에 정리한 이항정리 식의 좌변과 우변을 0에서 1까지 적분하면 등식이 성립해야 하므로 다음과 같이 정리될 수 있습니다.

오른쪽 식만 좀 더 정리해서 4배 하면 우리가 구하고자 하는 원주율을 구할 수 있겠습니다.


위 방법은 뉴턴이 설명한 방법 중의 하나입니다.
원주율, 파이를 계산하는 방법에 관한 글을 마칩니다.
'수학 이야기' 카테고리의 다른 글
| 고3 2024 6월 수학 모의고사 22번 해설 - 함수의 증가와 감소 (0) | 2023.06.02 |
|---|---|
| n축 합성함수 그래프 그리기, n축 스킬 (0) | 2023.04.17 |
| 2023 3월 모의고사 수학 22번 풀이 (0) | 2023.03.24 |
| sin 72도 는 어떻게 계산할 수 있을까? 삼각함수의 신비를 풀어보자 ft. 옥스퍼드 대학 수학 기출 (1) | 2023.03.05 |
| 특수 문자 수학 기호를 정리하다 (0) | 2023.01.28 |






