2021 수능 수학 나형 30번 풀이 - 미분가능성과 연속성
30번 문제에서 가장 핵심어는 실수 전체에서 "미분 가능하다"는 말.
어떤 함수가 미분이 가능하려면 다음과 같은 특징을 가지고 있어야 함.
1. 함수 그래프가 꺾긴 부분 없이 매끈하게 연결되어야 한다. 그림을 잘 그리지 못해 여기에 제시하지 못하므로 이것의 예시와 설명은 교과서를 참고해 보세요.
2. 우극한과 좌극한 값이 같아야 한다.
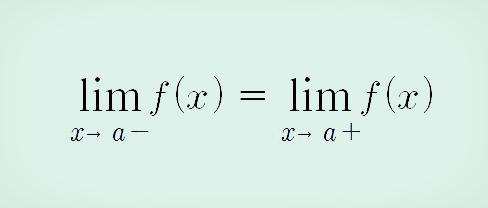
3. 우미분 값과 좌미분 값이 같아야 한다.

위 내용을 충분히 익혔으니 본격적으로 문제를 해결해 보겠습니다.
1. f(x)는 최고차항 계수가 1, g(x)는 일차함수, h(0) = 0이라는 조건에서 f(x) - g(x)는 다음과 같이 쓸 수 있습니다.
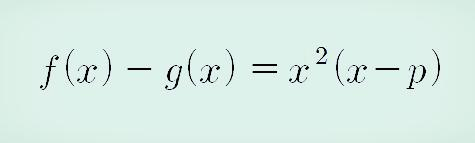
또한 x=0에서 f(x)와 g(x)가 접하려면 연속 및 미분이 되어야 하므로,
f(0) - g(0) = 0, f'(0) - g'(0) = 0이 되어야 한다.
2. 위 식을 정리하면 x가 1보다 작은 범위에서 h(x)는 다음과 같이 정리됩니다.
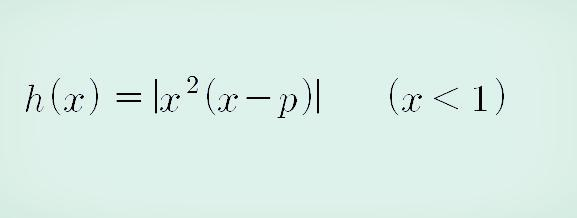
위 식에서 p는 1보다 커야합니다. 만약에 p가 1보다 작다면, 처음에서 미분조건 1번에서 그래프가 꺽긴 부분 없이 매끈해야 한다는 것이 성립하지 않기 때문입니다. 따라서 위의 h(x)는 절대값을 없앤 부분이 음수이므로 h(x)는 다음과 같이 절대값을 제거할 수 있습니다.




절대값 구하기 참고글
https://nous-temperature.tistory.com/431
절대값 계산, 절대값 구하기
이번 포스팅은 수학의 절대값에 관한 것입니다. 다음 문제를 풀어 보겠습니다. -3 위 문제를 해결하기 위해 먼저 "절대값"이란 무엇인지 알아보겠습니다. '절대값'이란 수직선 위의 점이 수직선
nous-temperature.tistory.com
3. x가 1보다 큰 범위에서는 h(x)는 1번 식을 이용하면 다음과 같이 계산됩니다.


4. 위의 2, 3에서의 h(x)는 x = 1에서 미분 가능해야 하므로, x=1에서 우극한과 좌극한 값이 같아야 하며, 우미분 값과 좌미분 값이 같아야 합니다.

즉,
g(1) - f(1) = f(1) + g(1)
g'(1) - f'(1) = f'(1) + g'(1)을 성립.
위 식을 풀면, f(1) = 0, g(1) = p-1
또한 f'(1) = 0이고, g'(1) = 2p-3
5. g(1) = p-1, g'(1) = 2p-3이므로
g(x) = (2p-3)(x-1) + p -1
g(2) = (2p-3)(2-1) + p -1 = 3p-4
*추가 설명: 위 말은 x =1, y = p-1을 지나고 직선의 기울기가 2p-3 [g'(1) = 2p-3]이므로 일차함수 g(x) = (2p-3)(x-1) + p-1이 되는 것임.
6. h(2) = 5다고 했으므로
f(2) + g(2) = 4(2-p) + 2g(2) = 5
8-4p + 2(3p-4) = 5
7. 위의 5, 6번의 방정식을 풀면 p = 5/2
8. 7에서 구한 p = 5/2를 위의 5번 결과와 4번의 밑의 밑에 있는 식에 대입하면 h(x)는 다음과 같음.
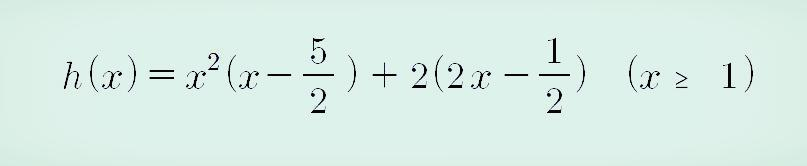
9. 구하고자 하는 h(4)는 위 식에 x 대신에 4를 대입하면 됩니다.
'수학 이야기' 카테고리의 다른 글
| 이차함수 넓이 공식, 이차함수 직선 넓이 (4) | 2020.12.20 |
|---|---|
| 유리함수 - 점근선 방정식을 나눗셈으로 구하기 (1) | 2020.12.12 |
| 다항식의 곱셈 (초등학교 곱셈 이용하는 방법) (8) | 2020.10.22 |
| 절대값 계산, 절대값 구하기 (5) | 2020.10.01 |
| 다항식의 나눗셈, 이렇게 풀어보세요. [고1 수준] (4) | 2020.09.22 |






