이차함수 넓이 공식, 이차함수 직선 넓이
지난 12월 3일에 실시한 수능 수학 나형 27번에 이차함수와 직선으로 둘러싸인 넓이를 구하라는 문제가 나왔습니다.
주관식 4점짜리로 그 비중에 작지 않은 문제였다고 생각하는데요.
그런데, 이 문제를 보면서 드는 생각, 수학도 가끔은 "암기 과목"이구나 하는 느낌이 들었던 것이 사실입니다. 이 문제를 낸 의도가 직접 적분 기호를 써서 일일이 풀어서 계산하는 것인지, 아니면 공식만 알고 있으면 해결하려는 의도로 출제한 것인지는 판단이 잘 안 섭니다.
하지만, 다음과 같이 이차함수와 직선으로 둘러싸인 넓이를 구하는 공식을 알고 있으면 나형 27번 문제는 개인적으로 공식을 몰랐을 때보다 적어도 10배는 시간이 단축되지 않았을까 해서 그 공식을 소개해 봅니다.
■ 두 함수가 만나는 점, 또는 근이 알파와 베타일 때 두 함수로 둘러싸인 넓이 공식


위 식을 유도해서 먼저 두 근이 알파와 베타이고, x축과 이차함수에 둘러싸인 부분의 넓이를 먼저 구해보겠습니다.


위의 이차함수가 x축에서 알파와 베타인 점에서 만난다는 말은 이 알파와 베타가 이차함수의 두 근이므로 위에 제시한 이차함수 일반식은 다음과 같이 쓸 수 있습니다.
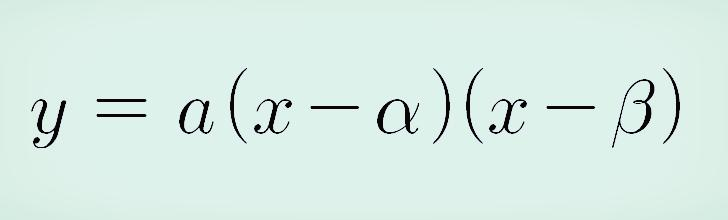
이제 위 식을 알파에서 베타까지 정적분 하면 넓이를 구할 수 있습니다.

위의 풀이 과정을 x축이 아닌 일반 일차함수와 이차함수의 근이 다음과 같은 것도 결국엔 위와 같은 풀이 과정을 거치면 다음과 같이 공식을 정리할 수 있습니다.
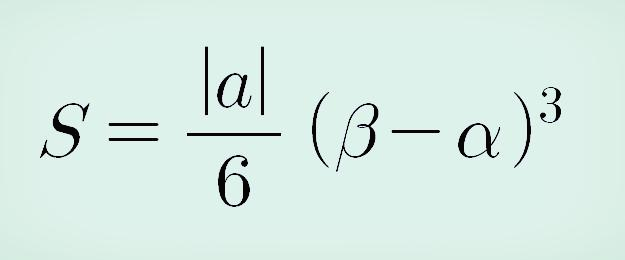
올해 수능 수학 나형 27번의 경우는 두 근이 0, 6이고 이차함수 계수 즉, a가 1이므로 위 식에 대입하면 간단하게 답이 나옵니다.
시간이 허락한다면, 이차함수와 이차함수가 둘러싼 넓이 공식, 3차 함수에서 둘러싸인 공식을 유도하는 방법도 추후 포스팅하겠습니다.
'수학 이야기' 카테고리의 다른 글
| 이차식 나머지 정리, 이차식 나머지 쉽게 구하기 (3) | 2021.02.13 |
|---|---|
| 삼차식으로 나눈 나머지, 3차식으로 나눈 몫과 나머지 (5) | 2021.02.07 |
| 유리함수 - 점근선 방정식을 나눗셈으로 구하기 (1) | 2020.12.12 |
| 2021 수능 수학 나형 30번 풀이 - 미분가능성과 연속성 (6) | 2020.12.05 |
| 다항식의 곱셈 (초등학교 곱셈 이용하는 방법) (8) | 2020.10.22 |






