다항식의 나눗셈과 최대공약수 구하는 법
요즘 초등학교 5학년 1학기 때, 최대공약수와 최소공배수를 배웁니다.
막내에게 관련 문제를 알려주다가, 아래와 같은 문제를 직접 만들어 보았습니다. 물론, 아래 문제는 초등학교 5학년 수준에서 숫자로 표시된 부분을 고등학교 1학년 수준에 맞게 다항식으로 바꾸어 문제를 만든 것인데, 혹시, 문제의 타당성 등이 어색하다면, 댓글 남겨 주세요. 검토해서 적절하게 고치도록 하겠습니다.

이 문제를 해결하기 위해서 먼저, 나눗셈과 나머지, 두 수의 최대공약수와 최소공배수의 특징에 대해서 알아보겠습니다.
1. 두 수의 나눗셈과 나머지의 관계식
아래와 같이 B를 A로 나누었을 때, 몫 Q, 나머지를 R이라고 한다면 A, B, Q, R의 관계식은 아래와 같이 쓸 수 있습니다.
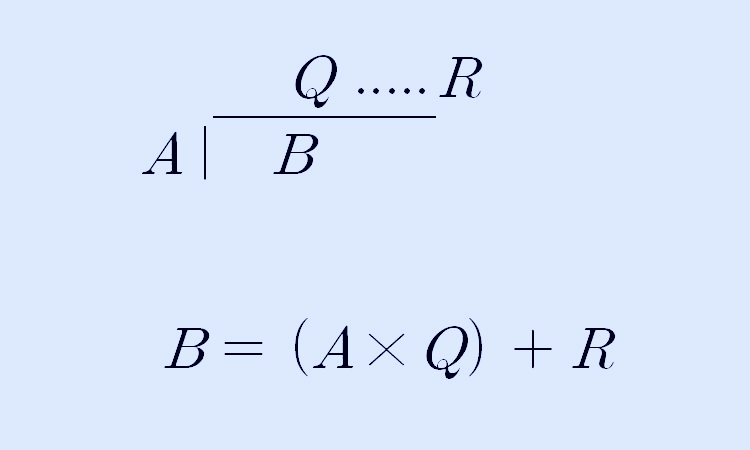
이제, 어떤 두 수, A와 B가 있을 때, 두 수의 최대공약수가 G라고 한다면, A와 B는 다음과 같이 쓸 수 있습니다.
2. 최대공약수, 최소공배수 사이의 관계식

a와 b가 서로소이면 최소공배수를 L이라고 하면 L= Gab입니다. 그리고, 두 수의 덧셈, 뺄셈, 곱셈을 최대공약수 G와 최소공배수 L을 써서 나타내면, A+B, A-B, AB는 다음과 같이 쓸 수 있습니다.

위 식은 두식의 뎃셈, 뺄셈, 곱셈에는 최대공약수 G를 이용해서 쓸 수 있으며, 특히 마지막 두 수의 곱은 최대공약수와 최소공배수의 곱으로 나타낼 수 있다는 것을 보여 줍니다.
3. 그러면, 맨 위에서 제시한 문제는 어떻게 해결할 수 있을까요?
먼저, 두 다항식의 몫을 각각 Q1, Q2라고 가정하고, 주어진 문제는 곱셈과 나머지 형태로 쓰면 다음과 같이 정리할 수 있습니다.

여기까지 풀었으면 오른쪽 항에 있는 나머지 3을 왼쪽 항으로 이항 시켜서 다음과 같이 쓸 수 있습니다.
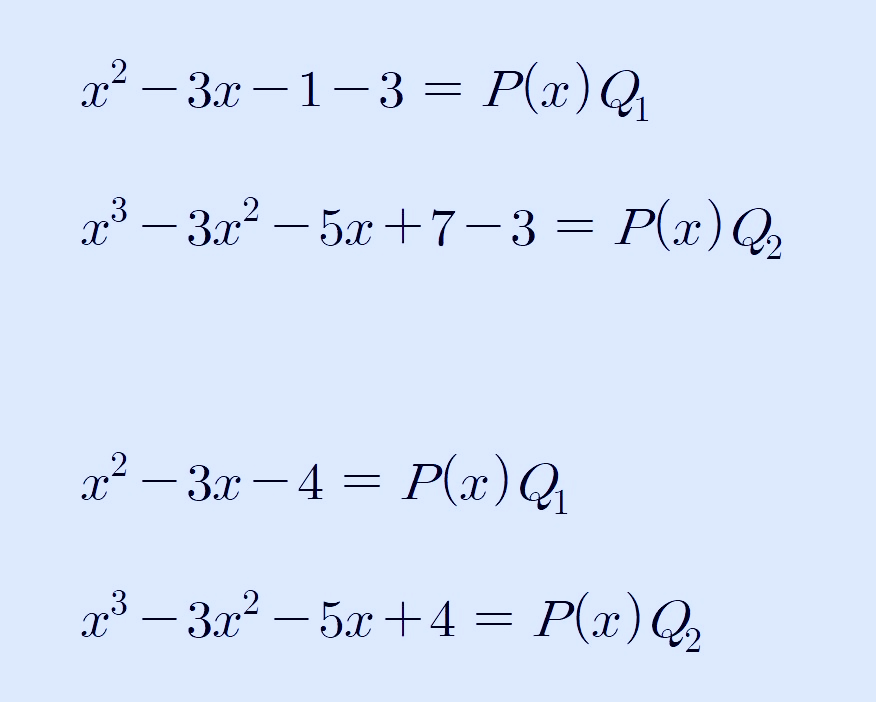
이렇게 써 놓고 보니, 나누었던 일차식 P(x)가 무엇으로 보이나요?
Q1과 Q2가 서로소라고 하면, P(x)는 바로 두 다항식의 최대공약수가 된다는 것을 알 수 있습니다. 즉, 이 문제에서 어떤 일치식은 나머지를 피제수에서 빼주면 바로 두 다항식의 "최대공약수"가 된다는 것입니다.
두 다항식은 인수 분해해서 정리하면 다음과 같습니다.
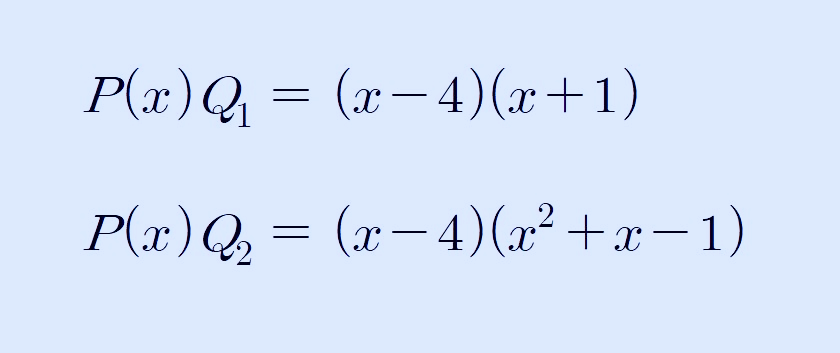
어떤 나누는 일차식은 위의 계산에서 P(x) = x-4가 됩니다. 따라서 구하고 하는 P(5) = 1이 되겠습니다.
어떤 다항식에서 나머지 정리와 최대공약수, 최소공배수의 특징을 이용하면 생각지도 못한 문제를 만들 수 있을지도 모릅니다. 이러한 문제의 기초는 아마도 초등학교 때 배운 내용을 일반적인 문자 식으로 확장해서 고등학교 수준에서는 이해는 것일 수 있습니다. 그렇기 때문에 수학이 어렵고 힘든 과목의 하나일지 모르지만, 어떤 개념에서 파생 및 확장하는 것을 이해하면 도움이 될지도 모를 일입니다.
오늘 글을 마칩니다.
'수학 이야기' 카테고리의 다른 글
| 알아 두면 유용한 미분 공식 모음 - 루트 x 미분 등 (0) | 2022.09.18 |
|---|---|
| 고3 2022 9월 모의고사 수학 22번 해설 (8월 31일 실시 모평) (0) | 2022.09.02 |
| 좌표 평면에서 두 점 사이의 거리 공식은 어떻게 구할까? (0) | 2022.08.22 |
| 바이오리듬과 삼각함수 주기 구하기 (0) | 2022.08.21 |
| 세상에서 가장 아름다운 수학 등식, 오일러 공식을 증명해 보자 (0) | 2022.08.20 |






