고3 2022 9월 모의고사 수학 22번 해설 (8월 31일 실시 모평)
삼차 함수 최고차 항의 계수가 1, x=3에서 극댓값이 8이라는 조건이 있습니다. 극대점을 지나는 y=8을 긋고 삼차 함수와 만나는 다른 한 점의 x 좌표를 p라고 한다면 그래프와 삼차 함수 f(x)는 다음과 같이 쓸 수 있습니다.
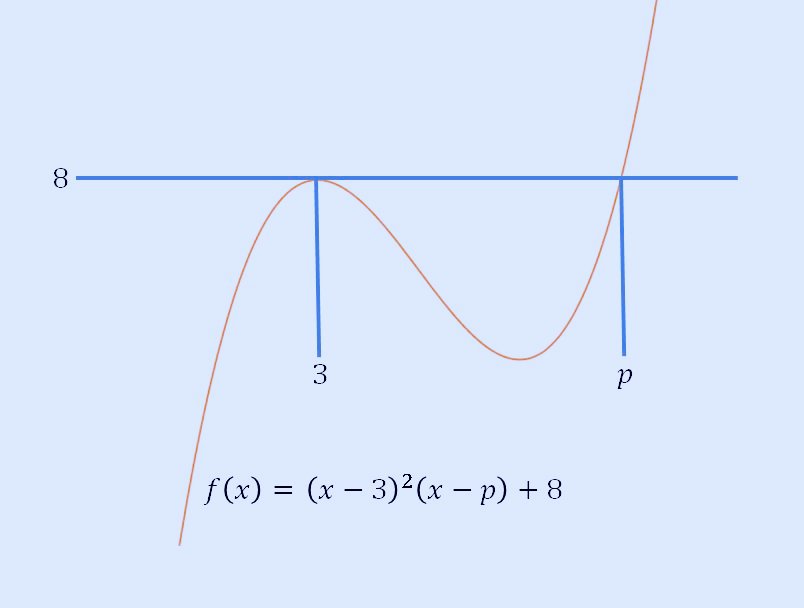
g(x)는 t보다 크거나 같으면 f(x) 값을 그대로 가지고, t보다 작으면 f(x)의 그래프를 x축 방향으로 꺾어 올려서 y=f(t)에서 대칭시켜야 한다는 말이 됩니다. 이는 x축과 평행한 선에서 t보다 작은 곳에서 위로 꺾어 올리라는 말인데, 두 함수를 더해서 2로 나누면 구할 수 있습니다. 따라서 f(x)의 그래프는 극솟값을 크기에 따라 다음 3가지로 정리할 수 있겠습니다. 문제의 조건에서 x축의 위치를 알아야 p의 값을 알 수 있기에, 지금까지 수능이나 모의고사에서 가장 많이 나온 그래프의 유형인 첫 번째 것으로 문제의 조건을 파악해 보겠습니다.

실근의 개수를 h(t)라고 했으므로 위 첫 번째 그래프부터 t의 값의 변화에 따라 실근이 어떻게 나오는지 알아보도록 합니다.
먼저, t가 삼차 함수 x축과 만나는 교점보다 작은 위치(왼쪽)에 있다면 아래와 같은 모습이 되고 g(x)는 근이 3개가 존재합니다.
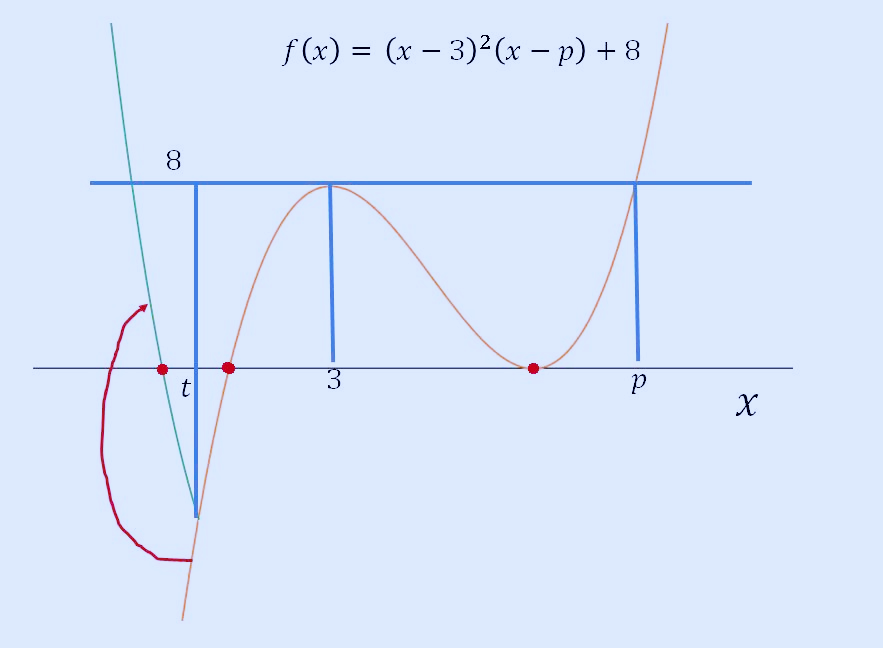
아래와 같이 t가 f(x)가 x축과의 교점이라면 아래의 그래프에서 g(x)=0의 실근이 2개가 됩니다. 따라서 3개에서 2개로 바뀌었으므로 불연속 점이 되겠네요.
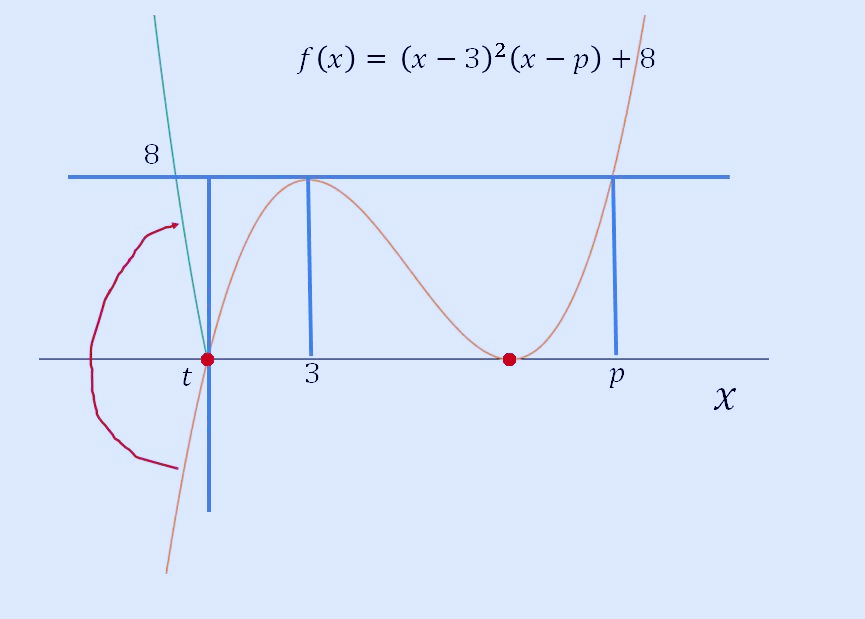
t가 x축 교점과 3 사이에 있다면 그래프는 다음과 같으며 실근은 1개가 됩니다. 이와 같이 t가 f(x) 변곡점 사이라고 한다면 꺾인 그래프와 x축이 만날 때까지 계속 실근은 1개가 될 것입니다. 여기서는 실근이 계속 1개이므로 연속입니다.
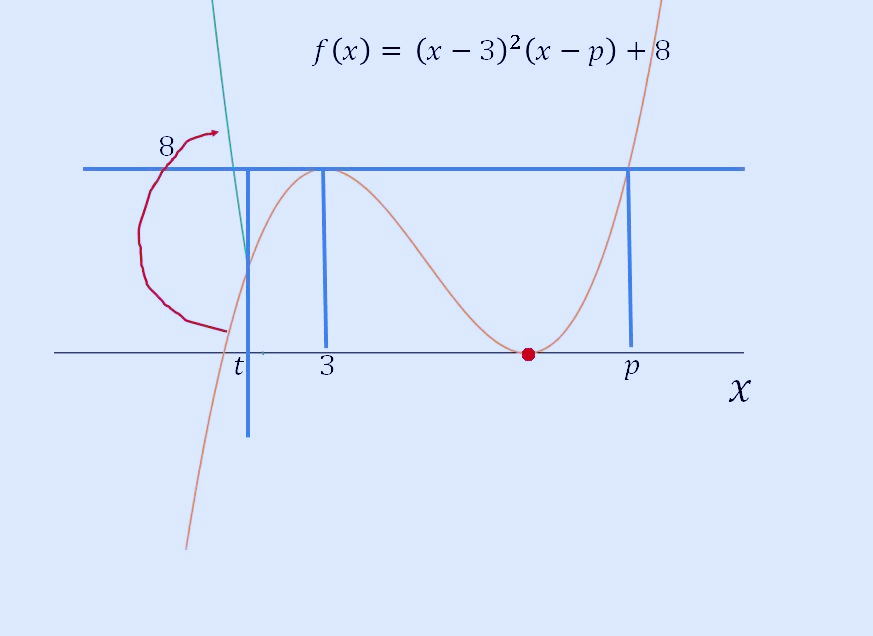
t가 f(x)의 변곡점이라면 실근이 아래의 그래프처럼 2개가 될 것입니다. t가 변곡점보다 크다면 초록색 볼록한 부분이 더 내려가기 때문에 실근이 3개가 되고, 여기에서 불연속이 됩니다.
t가 p라면 f(x)를 꺾어서 올리면 실근이 2개가 되고, p보다 약간 크면 실근이 3개임을 유추할 수 있으며, 이 점에서 불연속이 됩니다.
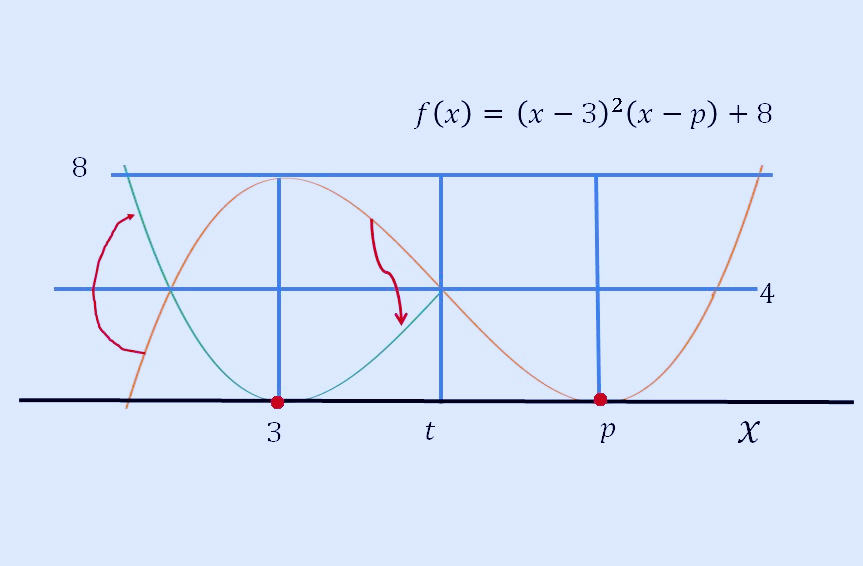
여기까지 보면 불연속점이 3개이므로 더 이상할 필요가 없겠습니다. 즉 위 그래프 유형은 성립할 수가 없겠네요.
이제 두 번째 그래프 유형을 위와 같은 방식으로 찾아보아야겠습니다.

t의 위치를 첫 번째 그래프 유형처럼 차례대로 구해 본다면, 실근의 개수가 4개, 3개, 2개, 3개 순서로 계산되기 때문에 불연속 점이 이 그래프 유형도 주어진 조건을 만족하지 않습니다.
이제 마지막 그래프가 남았네요.
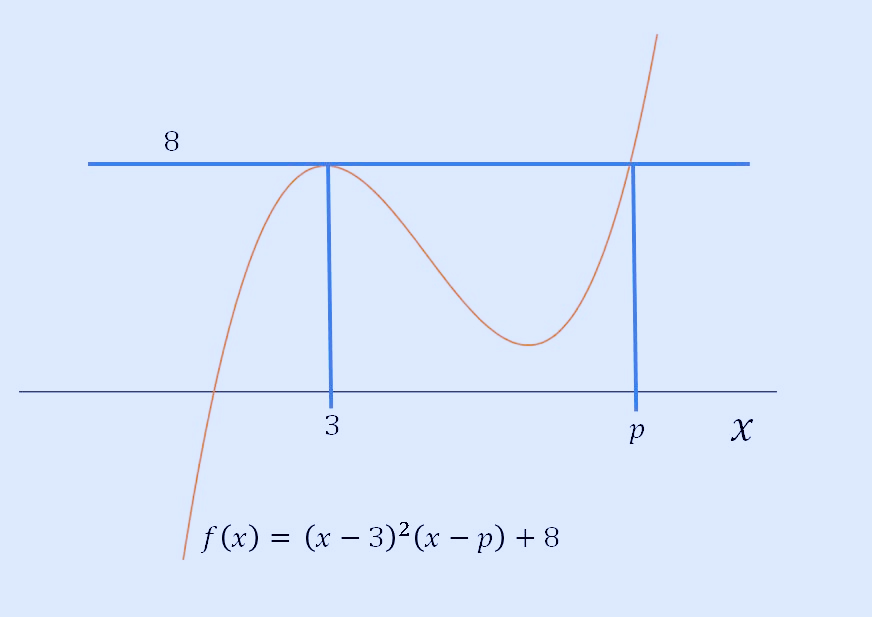
이 삼차 함수와 x축과 만나는 점을 t라고 한다면 g(x) 그래프는 다음과 같이 그릴 수 있으며 실근의 개수는 1개가 됩니다. 만약에 t가 더 왼쪽에 있다면 실근의 개수는 2개가 된다 것을 알 수 있습니다. 즉, 왼쪽부터 2개, 1개로 변하므로 여기서 불연속점이 됩니다.
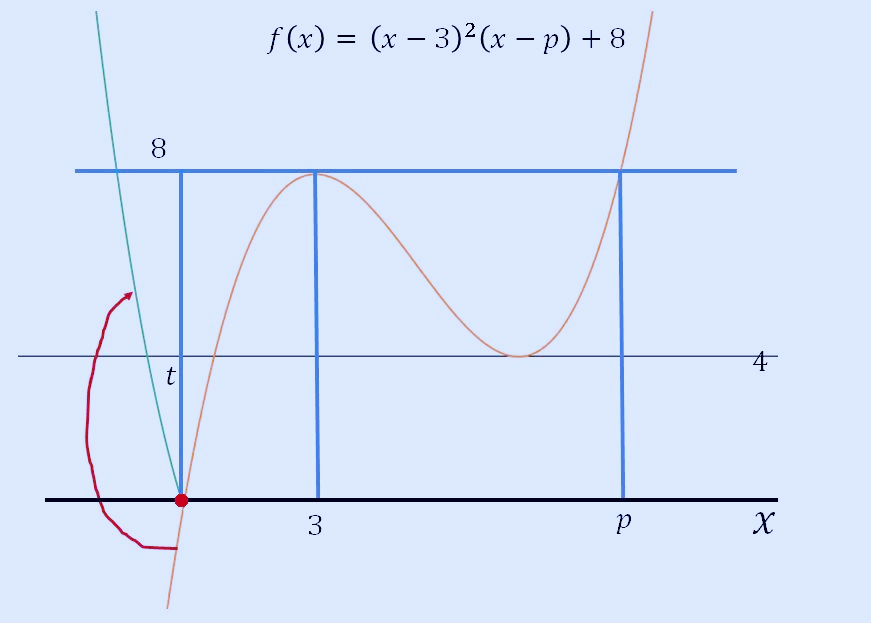
t가 만나는 점과 3 사이에 있다면 교점의 개수는 0개 됩니다.
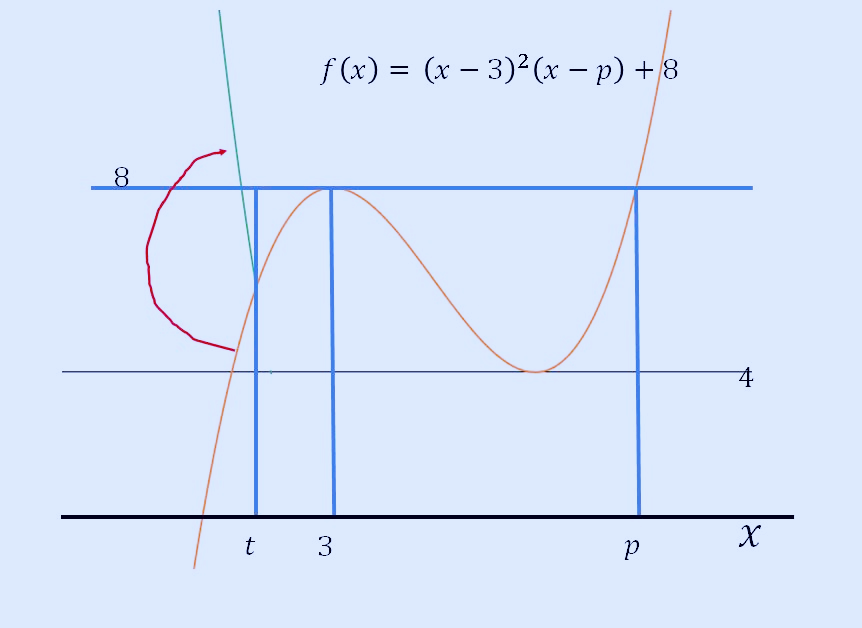
실근 개수가 계속 0이 되다가 극소점에 위치할 때, g(x)는 다음과 같이 실근을 하나 가지게 됩니다. 그러다가 t가 극소 점보다 오른쪽에 있으면 녹색의 볼록한 부분은 더 위로 올라가기 때문에 실근의 개수는 0이 됩니다. 즉 여기에서 불연속점이 하나 생기는 것입니다.
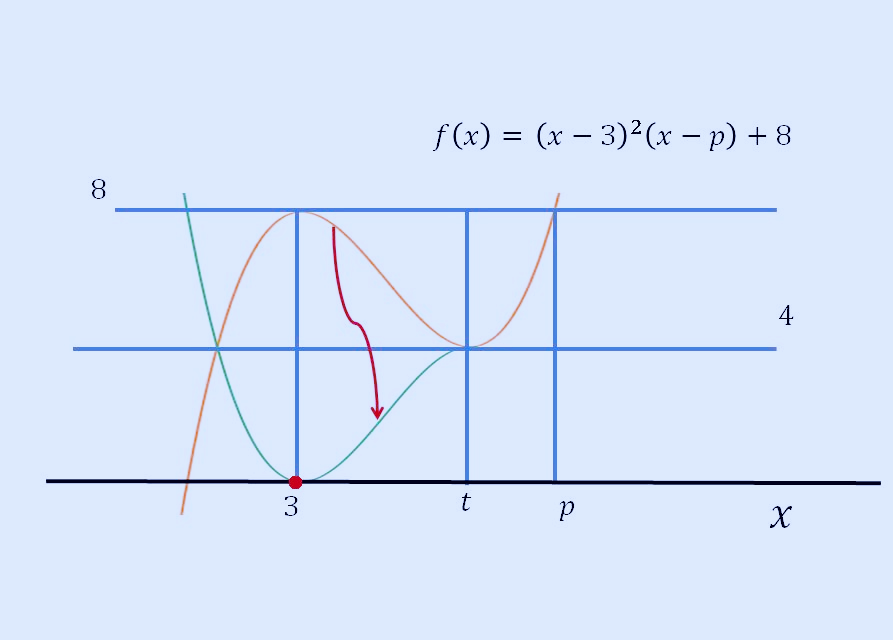
따라서 위 그래프가 되면, 불연속점이 2개가 되고 조건에 맞는 그래프가 됩니다.
위 그래프를 잘 보면, x=3에서 극댓값이 8이고 t에서 극솟값이 4이므로 두 값의 차이는 4가 됩니다. 따라서 두 t의 값은 다음 식으로 계산할 수 있습니다. (참고: 제 블로그 글 중에서 극대 극소 차 공식을 참고해 보세요.)
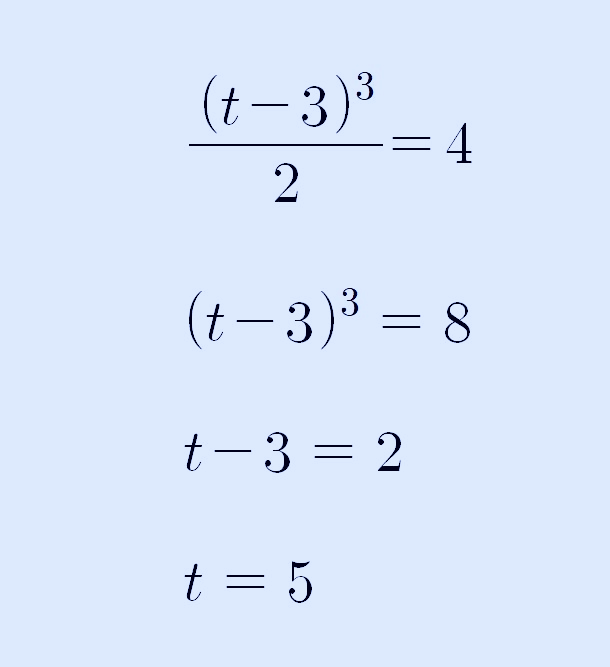
삼차 함수 비율 관계를 살펴보면, t=5이기 때문에 변곡점의 x좌표는 4가 되고, p=6이 됩니다. 따라서 아래 그림처럼 f(x)의 값이 완성됩니다. 구하고자 하는 f(8)의 값은 x대신에 8을 대입해서 계산하면 되겠습니다.

오늘 글을 마칩니다.
'수학 이야기' 카테고리의 다른 글
| 쌓기나무 개수 구하기 (0) | 2022.09.21 |
|---|---|
| 알아 두면 유용한 미분 공식 모음 - 루트 x 미분 등 (0) | 2022.09.18 |
| 다항식의 나눗셈과 최대공약수 구하는 법 (0) | 2022.08.25 |
| 좌표 평면에서 두 점 사이의 거리 공식은 어떻게 구할까? (0) | 2022.08.22 |
| 바이오리듬과 삼각함수 주기 구하기 (0) | 2022.08.21 |






